Question

A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of $\pi$.

Answer 1

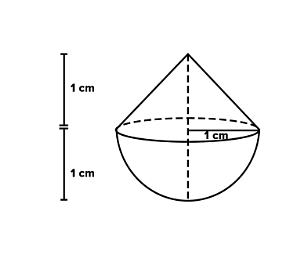
Given that,
Height (h) of conical part = Radius(r) of conical part = 1 cm
Radius(r) of hemispherical part = Radius of conical part (r) = 1 cm

Volume of solid = Volume of conical part + Volume of hemispherical part
$=\frac{1}{ 3}\pi 𝑟^2ℎ+\frac{2}{ 3}\pi 𝑟^3$

$=\frac{1}{ 3}\pi \times1^2\times1+\frac{2}{ 3}\pi \times1^3$

$=\pi \ 𝑐𝑚^3$