Question
Question: A solid hemisphere (m, R) has the moment of inertia about axis 1 (Diameter of hemisphere)  has the moment of inertia about axis 1 (Diameter of hemisphere)
A. 5mR2
B. 52mR2
C. 32mR2
D. 320173mR2
Solution
Hint: First step will be considering a disc shaped component parallel to the base of the solid hemisphere. Then we will find the moment of inertia of that disc about its center of mass. Then by using parallel axis theorem, we will find the moment of inertia about the axis 1. Then upon integrating the equations we got over the range 0 to R, we will get the required result.
Complete step by step solution:
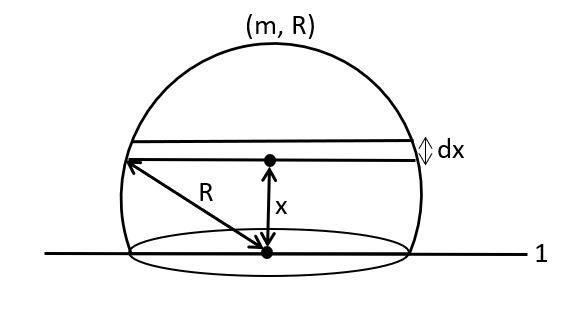
Let us consider a circular disc-shaped component of the solid hemisphere at a distance x from the axis 1 with radius y and width dx.
As the mass and radius of this hemispherical solid is m and R.
So, mass of the disc, dm=volume of hemispheremass of hemisphere×volume of the disc
⟹dm=32πR3m(πy2dx)
Let us take ρ=32πR3m.
Therefore, dm=ρ(πy2d) ………. (i)
Now, moment of inertia of the solid hemisphere about the axis 1 can be given by the parallel axis theorem as,
I1=Icm+mx2, where Icm is the moment of inertia of the disk about its centre of mass.
Therefore, dI1=(dm)4y2+(dm)x2
Now we will integrate both sides of the equation for the range 0 to R.
⟹I1=∫0R(dm)4y2+∫0Rdmx2
Putting the value of dm from equation (i)
⟹I1=∫0R(ρπy2dx)4y2+∫0R(ρπy2dx)x2
=4ρπ∫0R(R2−x2)dx+ρy∫0R(R2X2−x4)dx
=4ρπ[R5+5R5−2R23R3]+[ρπR2(3R3)−ρπ(5R5)]
=4ρπR5[1+51−32]+ρπR5[31−51]
=ρπR5(154)
Since, ρ=32πR3m.
∴I1=2πR33m.πR5415=52mR2.
Hence, option b is the correct answer.
Note: Moment of inertia of a disc is a basic thing applied here and should be remembered. One may forget to use the parallel axis theorem while solving such types of questions. The axis of solid hemisphere about which the moment of inertia has been asked should be parallel to the axis of the disc.
