Question

A solid hemisphere is just pressed below the liquid, the value of $\dfrac{{{F_1}}}{{{F_2}}}$ is (where ${F_1}$ and ${F_2}$ ) are the hydrostatic force acting on the curved and flat surfaces of the hemisphere (Neglect atmospheric pressure).
A. $\dfrac{1}{2}$
B. $\dfrac{2}{3}$
C. $\dfrac{1}{3}$
D. None of these

Answer 1

Recall the concept of buoyancy. The other name for buoyancy is upthrust force. It is basically an upward force exerted by a fluid. This force opposes the weight of a partially or a fully immersed object in the Fluid. The pressure at the bottom of a column of the fluid is greater than that on the top of the column.

Complete answer:

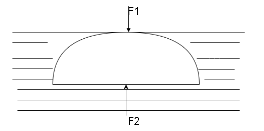
Step I:
The pressure at the bottom of an object submerged in a fluid is greater than that at the top of the
object. This pressure difference results in a net upward force on the object.
Step II:
The buoyant force can be calculated by adding all the forces acting on all the sides of the object. The
force ${F_2}$ on the bottom surface will act in an upward direction. The formula used is:
$\Rightarrow$ ${F_2} = P \times A$
Where $P = \rho GH$
Where Rho$\rho$ is the density
G is the gravitational acceleration and
H is the height that is equal to R in this case.
$\Rightarrow$ ${F_2} = (\rho \times G \times R) \times \pi {R^2}$
Step III:
Similarly the force ${F_1}$ can also be calculated. The force acting at the top surface will point downwards.
The force acting above the curved surface of the sphere is given by ${F_1}$ . The formula to calculate force
remains the same but the height considered is the area in which the fluid is applying pressure on the
particle.
$\Rightarrow$ ${F_1}$ = weight of liquid above curved surface
$\Rightarrow$ ${F_1} = \rho \times (\pi {R^2} - R - \dfrac{2}{3}\pi {R^3}) \times G$
$\Rightarrow$ $F_1 = \dfrac{1}{3}\rho G\pi {R^3}$
Calculating the ratio,
$\Rightarrow$ $\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{1}{3}$

$\therefore$ The required ratio is $\dfrac{1}{3}$. Hence, Option C is the correct answer.

Note:
It is to be noted that the Archimedes principle is known as the physical law of buoyancy. It helps in
determining whether the object will float or sink. If the weight of an object is less than that of the
displaced fluid then the object rises. But if the weight of an object dispersed is more than that of the
fluid, then the object will sink.