Question

A solid cylinder rolls without slipping on an inclined plane at an angle $\theta$. Find the linear acceleration of the cylinder. Mass of the cylinder is M.
(A). $a=\dfrac{1}{3}g\sin \theta$
(B). $a=\dfrac{2}{3}g\sin \theta$
(C). $a=\dfrac{1}{3}g\cos \theta$
(D). $a=\dfrac{2}{3}g\cos \theta$

Answer 1

The cylinder is rolling down an inclined plane therefore, it possesses both rotational and translatory motion. As its motion is in a plane, it will have forces acting along the x- axis as well as along the y-axis. Resolving the forces acting on it, we can form equations for it for rotational as well as translatory and use it to find the value of acceleration.

Formulas used:
$mg\sin \theta -F=ma$
$\alpha =\dfrac{a}{r}$
$Fr=I\alpha$

Complete step-by-step solution:

A cylinder is rolling without slipping on an inclined surface inclined at an angle $\theta$. The forces acting the cylinder will be-

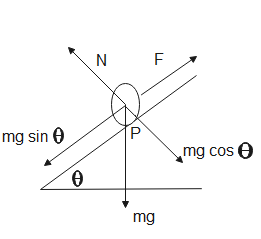
From the given figure, we have,
$N=mg\cos \theta$ - (1)

The forces acting along the inclined are-
$mg\sin \theta -F=ma$
$\therefore F=mg\sin \theta -ma$ - (2)

For the condition of rolling without slipping, the velocity at the point in contact with the surface must be equal to the velocity of the centre of mass.
$\begin{aligned} & {{v}_{cm}}={{v}_{\tau }} \\\ & \therefore v={{v}_{\tau }} \\\ \end{aligned}$
Here,${{v}_{cm}}$ is the velocity of the centre of mass
${{v}_{\tau }}$ is the velocity of point P.

Therefore,
$\omega =\dfrac{v}{r}$, $\omega$ is the angular velocity
Similarly,
$\alpha =\dfrac{a}{r}$
Here,
$\alpha$ is the angular acceleration
$a$ is the linear acceleration
$r$ is distance from the axis of rotation.

For its angular motion,
$\tau =I\alpha$
Here,
$\tau$ is the torque
$I$ is the moment of inertia
$\therefore Fr=I\alpha$

We substitute the value of $F$ from eq (2) to get,
$\begin{aligned} & (mg\sin \theta -ma)r=\dfrac{1}{2}m{{r}^{2}}\times \dfrac{a}{r} \\\ & \Rightarrow mgr\sin \theta -mar=\dfrac{mar}{2} \\\ & \Rightarrow mgr\sin \theta =\dfrac{3}{2}mar \\\ & \therefore a=\dfrac{2}{3}g\sin \theta \\\ \end{aligned}$
Therefore, the acceleration of the solid cylinder when rolling without slipping is $\dfrac{2}{3}g\sin \theta$.

Therefore, the correct option is (B).

Note:
The linear velocity at point P is tangential to the motion of the cylinder. For the cylinder to roll without slipping, the total velocity of point P must be zero. ${{v}_{cm}}$and${{v}_{\tau }}$ are in opposite directions. The normal reaction is the force acting between two surfaces which prevent them from passing through each other.