Question

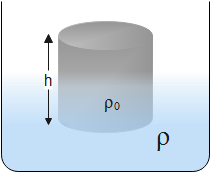
A solid cylinder of density $\rho_0$, cross-section area A and length l floats in a liquid of density $\rho \left( >{{\rho }_{0}} \right)$ with its axis vertical, as shown. If it is slightly displaced downward and released, the time period will be.

A. $2\pi \sqrt{\dfrac{l}{g}}$
B. $2\pi \sqrt{\dfrac{{{\rho }_{0}}l}{\rho g}}$
C. $2\pi \sqrt{\dfrac{\rho l}{{{\rho }_{0}}g}}$
D. $2\pi \sqrt{\dfrac{l}{2g}}$

Answer 1

Due to difference in pressure at different heights in a fluid, an upward force acts on a body submerged in it which is known as buoyant force. This force is linearly proportional to displaced volume of liquid and its density. Expression of the buoyant force can be used to determine the frequency of the cylinder and therefore, its time period as well.

Complete step by step answer:
When any body is floating in a liquid, it is in equilibrium. At equilibrium the weight of the body is balanced by buoyant force due to the liquid. When it is slightly displaced downward, the upward force on it increases due to increase in buoyant force, for more displacement of liquid. Buoyant force is directly proportional to density of the liquid and volume of the liquid displaced.
${{F}_{b}}=-\rho Vg$
Negative sign here shows that the force is opposite to the direction of displacement. Since, volume of the liquid displaced is equal to the volume of solid cylinder submerged after displacement. Therefore,
$V=Ax$
Substituting this, we have
${{F}_{b}}=-\rho gAx$
This force causes acceleration, in the cylinder, of magnitude
$a=\dfrac{{{F}_{b}}}{M}=\dfrac{-\rho Axg}{M}$
This acceleration is similar to spring force acceleration and can also be written as
$a=-{{\omega }^{2}}x$
Where $\omega =\dfrac{2\pi }{T}$ is the frequency of the solid cylinder. Equating both equations, we have
$-\dfrac{\rho Ag}{M}x=-{{\omega }^{2}}x$
This implies that,
$\omega =\sqrt{\dfrac{\rho Ag}{M}}$
Mass of the cylinder can also be written as $M={{\rho }_{0}}Al$. Substituting,
$\omega =\sqrt{\dfrac{\rho g}{{{\rho }_{0}}l}}$
This implies that,
$T=\dfrac{2\pi }{\omega }=2\pi \sqrt{\dfrac{{{\rho }_{0}}l}{\rho g}}$
Hence, option B is correct.

Note: The buoyant force acts due to difference in pressures at different heights in a fluid. When the object floats on the fluid, it is in equilibrium. If the density of the object is more than the density of the liquid, it sinks in the liquid otherwise not.