Question

A solid cylinder has mass M, radius R and length l. its moment of inertia about an axis passing through its centre and perpendicular to its own axis is,
$\begin{aligned} & \text{A}\text{. }\dfrac{2M{{R}^{2}}}{3}+\dfrac{M{{l}^{2}}}{12} \\\ & \text{B}\text{. }\dfrac{M{{R}^{2}}}{3}+\dfrac{M{{l}^{2}}}{12} \\\ & \text{C}\text{. }\dfrac{3M{{R}^{2}}}{4}+\dfrac{M{{l}^{2}}}{12} \\\ & \text{D}\text{. }\dfrac{M{{R}^{2}}}{4}+\dfrac{M{{l}^{2}}}{12} \\\ \end{aligned}$

Answer 1

Hint : To solve this question consider a disc of width dx on the cylinder. Find the moment of inertia of the disc about the axis of the cylinder. Then find its moment of inertia about the axis passing through the centre of the cylinder perpendicular to its axis. It can be done by the parallel axis theorem. Then we can find the moment of inertia of the whole cylinder by integrating the obtained value.

Complete step by step solution :

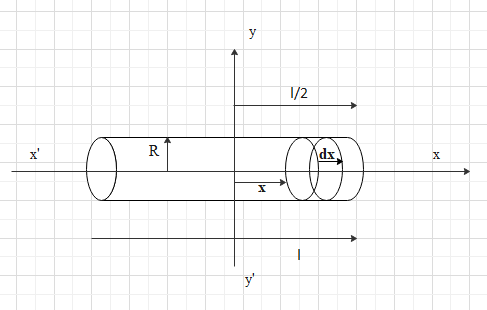
Let, xx’ is the axis of the cylinder and yy’ be the axis passing through the centre and perpendicular to the xx’ axis.
The mass of the cylinder is M.
The radius of the cylinder is R.
The length of the cylinder is l.
Mass per unit length of the cylinder is given as, $\dfrac{M}{l}$
Consider a small disc about the diameter of the cylinder of width dx.
Let the distance of the disc from the yy’ axis is x.
So, we can say that the mass of the disc is $m=\dfrac{M}{l}dx$
The moment of inertia of the disk about the diameter of the rod is, $\dfrac{\left( \dfrac{M}{l}dx \right){{R}^{2}}}{4}$
From the parallel axis theorem, we can find the moment of inertia of the disk about the yy’ axis as,
$=\dfrac{\left( \dfrac{M}{l}dx \right){{R}^{2}}}{4}+\left( \dfrac{M}{l}dx \right){{x}^{2}}$
Now, the moment of inertia of the cylinder can be found out by integrating the moment of inertia of the disk in the limit from $-\dfrac{l}{2}$ to $\dfrac{l}{2}$ .
So, the moment of inertia of the cylinder about the yy’ axis,
$\begin{aligned} & I=\int\limits_{\dfrac{-l}{2}}^{\dfrac{l}{2}}{\left( \dfrac{M}{l}dx \right)\dfrac{{{R}^{2}}}{4}+}\int\limits_{\dfrac{-l}{2}}^{\dfrac{l}{2}}{\left( \dfrac{M}{l}dx \right){{x}^{2}}} \\\ & I=\dfrac{M}{l}\dfrac{{{R}^{2}}}{4}\int\limits_{\dfrac{-l}{2}}^{\dfrac{l}{2}}{dx+\dfrac{M}{l}\int\limits_{\dfrac{-l}{2}}^{\dfrac{l}{2}}{{{x}^{2}}dx}} \\\ & I=\dfrac{M}{l}\dfrac{{{R}^{2}}}{4}\left[ x \right]_{-\dfrac{l}{2}}^{\dfrac{l}{2}}+\dfrac{M}{l}\left[ \dfrac{{{x}^{3}}}{3} \right]_{-\dfrac{l}{2}}^{\dfrac{l}{2}} \\\ & I=\dfrac{M}{l}\dfrac{{{R}^{2}}}{4}\left[ \dfrac{l}{2}-\dfrac{-l}{2} \right]+\dfrac{M}{l}\left[ \dfrac{{{\left( \dfrac{l}{2} \right)}^{3}}}{3}-\dfrac{{{\left( -\dfrac{l}{2} \right)}^{3}}}{3} \right] \\\ & I=\dfrac{M}{l}\dfrac{{{R}^{2}}}{4}l+\dfrac{M}{l}\dfrac{1}{3}\left( \dfrac{{{l}^{3}}}{4} \right) \\\ & I=\dfrac{M{{R}^{2}}}{4}+\dfrac{M{{l}^{2}}}{12} \\\ \end{aligned}$
So, the moment of inertia of the cylinder about an axis passing through its centre and perpendicular to its own axis is $\dfrac{M{{R}^{2}}}{4}+\dfrac{M{{l}^{2}}}{12}$.
The correct option is (D).

Note : We can find the moment of inertia of bodies with the help of the parallel axis theorem and the perpendicular axis theorem. According to the parallel axis theorem, the moment of inertia of the body about an axis parallel to the body is equal to the sum of the moment of inertia of the body about an axis passing through its centre and the product of the mass of the body and the square of the distance between the axis.