Question

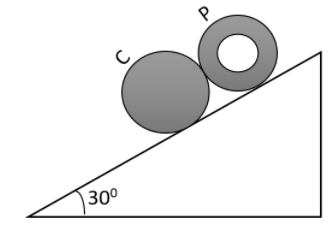
A solid cylinder C and a hollow pipe P of the same diameter are in contact when they are released from rest as shown in the figure on a long incline plane. The cylinder C and pipe P rolls down without slipping. Calculate the clear gap $\left( \text{in }m \right)$ between them after $23$ seconds.

Answer 1

The difference of the sine component of the gravitational force acting on the bodies and the frictional force will give the amount of force at which the body is rolling down. As the body is rolling, both the rotational as well as translational motion has been there. This information will help you in solving this question.

Complete answer:
The resultant force of the motion of the body is given as,
$mg\sin \theta -f=ma$
Where $m$ be the mass of the body, $\theta$ be the angle of inclination, $g$ be the acceleration due to gravity, $f$ be the frictional force acting on the body and $a$be acceleration of the object.
The torque at which the body is rotating can be written by the equation,
$\tau =I\alpha$
And the angular acceleration is related to the rotational acceleration as,
$a=\alpha r$
Therefore the value of frictional force will be,
$\begin{aligned} & \tau =r\times f \\\ & \Rightarrow f=\dfrac{\tau }{r}=\dfrac{I\alpha }{r} \\\ \end{aligned}$
Substituting this in the equation will give,
$mg\sin \theta -\dfrac{I\alpha }{r}=ma$
Substituting the value of angular acceleration in it,
$mg\sin \theta =\dfrac{Ia}{{{r}^{2}}}+ma$
Rearranging the equation,
$a=\dfrac{mg\sin \theta }{\left( \dfrac{I}{{{r}^{2}}}+m \right)}$
The moment of inertia of the solid cylinder should be,
$I=\dfrac{1}{2}m{{r}^{2}}$
Therefore the acceleration of the solid cylinder can be,
${{a}_{sc}}=\dfrac{mg\sin \theta }{\left( \dfrac{\dfrac{1}{2}m{{r}^{2}}}{{{r}^{2}}}+m \right)}=\dfrac{2}{3}g\sin \theta$
The moment of inertia of the hollow cylinder should be,
$I=m{{r}^{2}}$
Therefore its acceleration will be,
${{a}_{hc}}=\dfrac{mg\sin \theta }{\left( \dfrac{m{{r}^{2}}}{{{r}^{2}}}+m \right)}=\dfrac{1}{2}g\sin \theta$
The relative acceleration between them will be,
${{a}_{r}}=\dfrac{2}{3}g\sin \theta -\dfrac{1}{2}g\sin \theta =\dfrac{1}{6}g\sin \theta =\dfrac{g}{12}$
The time taken is given as,
$t=2\sqrt{3s}$
The gap after this much time can be written as,
$s=\dfrac{1}{2}a{{t}^{2}}$
Substituting the values in it will give,
$s=\dfrac{1}{2}\times \dfrac{g}{12}\times {{\left( 2\sqrt{3} \right)}^{2}}=5s$
Answers have been found.

Note:
Moment of inertia is otherwise known as the rotational inertia can calculate the torque required for a specific angular acceleration with respect to a rotational axis. This is somewhat similar to the mass which determines the linear acceleration.