Question
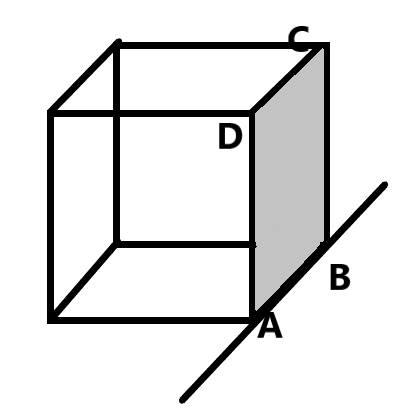
Question: A solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure...
A solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about the fixed axis AB. A bullet of mass m is very less than M and speed v is shot horizontally at the face opposite to ABCD at a height h above the surface to impart the cube an angular speed ωc so that the cube just topples over. (Note: the moment of inertia of the cube about an axis perpendicular to the face and passing through the centre of mass is (32Ma2). Then, ωc is:
Solution
We have to use the relation between the moment of inertia of the given mass about the axis AB and the angular velocity due to the force at which the bullet hits the opposite face of the face ABCD of the given solid cube as per the figure.
Complete answer:
Let us consider the solid cube which can rotate about the axis AB as shown in the figure. A bullet of mass ‘m’ strikes the opposite side of the face ABCD with a velocity ‘v’ which topples the solid cube about the axis AB. We know that the moment of inertia is the rotational analog of mass. It is the quantity of mass which causes the solid to rotate along the given axis. It is generally given as -
I=MR2
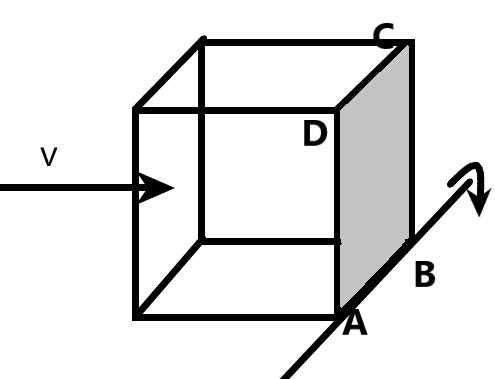
In the given situation, the moment of inertia needs to be calculated using the Parallel axis theorem as –
& I={{I}_{cm}}+m{{a}^{2}} \\\ & \Rightarrow I=\dfrac{2}{3}M{{a}^{2}}+M{{a}^{2}} \\\ & \Rightarrow I=\dfrac{8}{3}M{{a}^{2}} \\\ \end{aligned}$$ Where $${{I}_{cm}}$$ is the moment of inertia along the centre of mass. Now, let us calculate the angular velocity possessed by the solid cube when hit by a bullet by using the conservation of energy. The energy due to the moment of inertia and the potential energy difference can be equated as – $$\begin{aligned} & \dfrac{1}{2}I{{\omega }_{0}}^{2}=Mg({{h}_{f}}-{{h}_{i}}) \\\ & \Rightarrow \dfrac{1}{2}\dfrac{8}{3}M{{a}^{2}}{{\omega }_{0}}^{2}=Mg({{h}_{f}}-{{h}_{i}}) \\\ & \Rightarrow \dfrac{4}{3}{{a}^{2}}{{\omega }_{0}}^{2}=g({{h}_{f}}-{{h}_{i}}) \\\ & \Rightarrow {{\omega }_{0}}^{2}=\dfrac{3g({{h}_{f}}-{{h}_{i}})}{4{{a}^{2}}} \\\ & \Rightarrow {{\omega }_{0}}=\dfrac{\sqrt{3g({{h}_{f}}-{{h}_{i}})}}{2a} \\\ & \text{but,} \\\ & \text{(}{{\text{h}}_{f}}-{{h}_{i}})=(\sqrt{2}-1)a \\\ & \Rightarrow {{\omega }_{0}}=\sqrt{\dfrac{3g(\sqrt{2}-1)}{4a}} \\\ \end{aligned}$$ This is the required angular velocity. **So, the correct answer is “Option D”.** **Note:** We can use the parallel axis theorem when the moment of inertia of a parallel side and the moment of inertia about the centre of mass is already known. The perpendicular axes theorem is used to find the moment of inertia about a third axis which is perpendicular to two given axes.