Question

A solid consists of a cone on top of a cylinder with a radius equal to that of the cone. The height of the cone is 33 and the height of the cylinder is 13. If the volume of the solid is $256\pi$, what is the area of the base of the cylinder?

Answer 1

We first assume the radius as $r$ for both cone and the cylinder to calculate the total volume of the solid. We equate it with $256\pi$ and solve the equation. We then find the area of the base of the cylinder which is equal to $\pi {{r}^{2}}$ square units.

Complete step by step answer:
The radius of the base of the cone and the cylinder is same. Let us assume the radius as $r$.The height of the cone is 33 and the height of the cylinder is 13. We assume the heights as ${{h}_{1}}=33,{{h}_{2}}=13$. The total volume of the solid is $256\pi$.

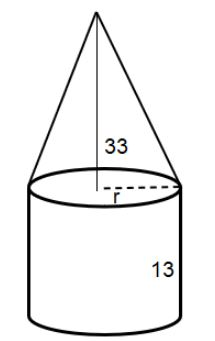
We find individual volumes. The formula of volumes for cone and cylinder are $\dfrac{\pi {{r}^{2}}{{h}_{1}}}{3}$ and $\pi {{r}^{2}}{{h}_{2}}$ respectively. The area of the base of the cylinder is $\pi {{r}^{2}}$ square units.Therefore, the equality with $256\pi$ gives, $\dfrac{\pi {{r}^{2}}{{h}_{1}}}{3}+\pi {{r}^{2}}{{h}_{2}}=256\pi$.
Putting the values, we get

$$\Rightarrow 11{{r}^{2}}+13{{r}^{2}}=256 \\\ \Rightarrow 24{{r}^{2}}=256 \\\$$

We simplify the equation to find the value of $\pi {{r}^{2}}$.

\therefore \pi {{r}^{2}}=\dfrac{256\pi }{24}=33.51 $$ **Therefore, the area of the base of the cylinder is $$33.51$$ square units.** **Note:** We need to be careful about the difference between height and slant height.The slant height is used for the lateral surface area of the cone. In the case of total surface area, we add one base area instead of two.