Question

A solid $AB$ has $NaCl$ structure. If the radius of cation ${A^ + }$ is $170pm$, then the maximum possible radius of the anion ${B^ - }$ is:
A. $397.4pm$
B. $347.9pm$
C. $210.9pm$
D. $410.6pm$

Answer 1

Every solid has its fixed crystal structure, this crystal structure is composed of small unit cells, which together gives birth to a crystal structure. The atoms present in each crystal structure have a fixed ratio of their atomic radii range.

Complete step by step answer:
The 3D arrangement of atoms is known as unit cell which can be repeatedly joined together to form a large crystal. Basically when the small unit cells are combined repeatedly they form a lattice, these lattices are defined on the basis of connectivity of atoms and their positions in a unit cell. The position f atom is known as its lattice point. A crystal structure consists of same group of atoms positioned around each and every lattice point. There are 14 bravais lattices defined for the three dimensional systems.
$NaCl$ is one of the crystal structures which is defined for a cation and an anion such as $N{a^ + }$ and $C{l^ - }$ . Sodium chloride has a cubic unit cell. The crystalline structure of sodium chloride is face centered cubic. The total number of ions present in the unit cell are eight, half of them are cations and half of them are anions.
The crystal structure of sodium chloride is as follows:

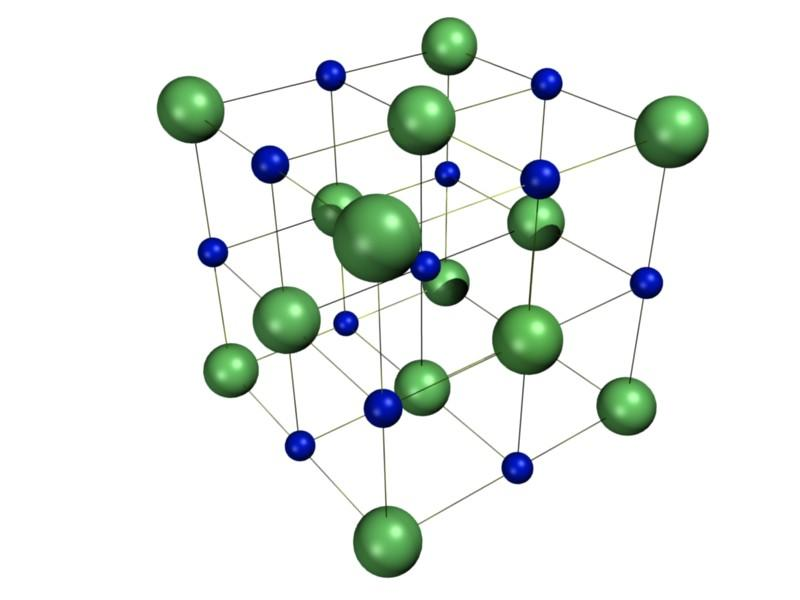
All the particles present at corners and face centers are chloride ions ($C{l^ - }$).
So the total number of $C{l^ - }$ = $8 \times \dfrac{1}{8} + 6 \times \dfrac{1}{2} = 4$
And the remaining particles are sodium ions which are present in octahedral voids,
Number of $N{a^ + }$ = $4$
And we know that radii ratio cations and anions ranges from $0.414 - 0.732$
$\Rightarrow \dfrac{{{{\text{r}}_{{{\text{A}}^{\text{ + }}}}}}}{{{{\text{r}}_{{{\text{B}}^{\text{ - }}}}}}} = 0.414$ to gain maximum possible radius of anion.
We have provided the radius of cation ${A^ + }$ i.e. $170pm$
By putting this value in above formula we get;
$\Rightarrow \dfrac{{170}}{{{{\text{r}}_{{{\text{B}}^{\text{ - }}}}}}} = 0.414$
$\Rightarrow {{\text{r}}_{{{\text{B}}^{\text{ - }}}}} = \dfrac{{170}}{{0.414}}$
$\Rightarrow {{\text{r}}_{{{\text{B}}^{\text{ - }}}}} = 410.6pm$
Hence the maximum possible radius of anion $410.6pm$

So, Option D is correct.

Note: The ratio of radii varies according to the atoms and the crystal lattice, so a definite range is decided for the ratio of atomic radii. To find the maximum possible value of anionic radii the minimum value of the atomic radii ratio is taken.