Question

A solenoid of inductance L and resistance r is connected in parallel to a resistance R. A battery of emf E and of negligible internal resistance is connected across this parallel combination as shown in figure. The circuit is in steady state. At time t = 0, switch S is opened. Choose the correct option(s).

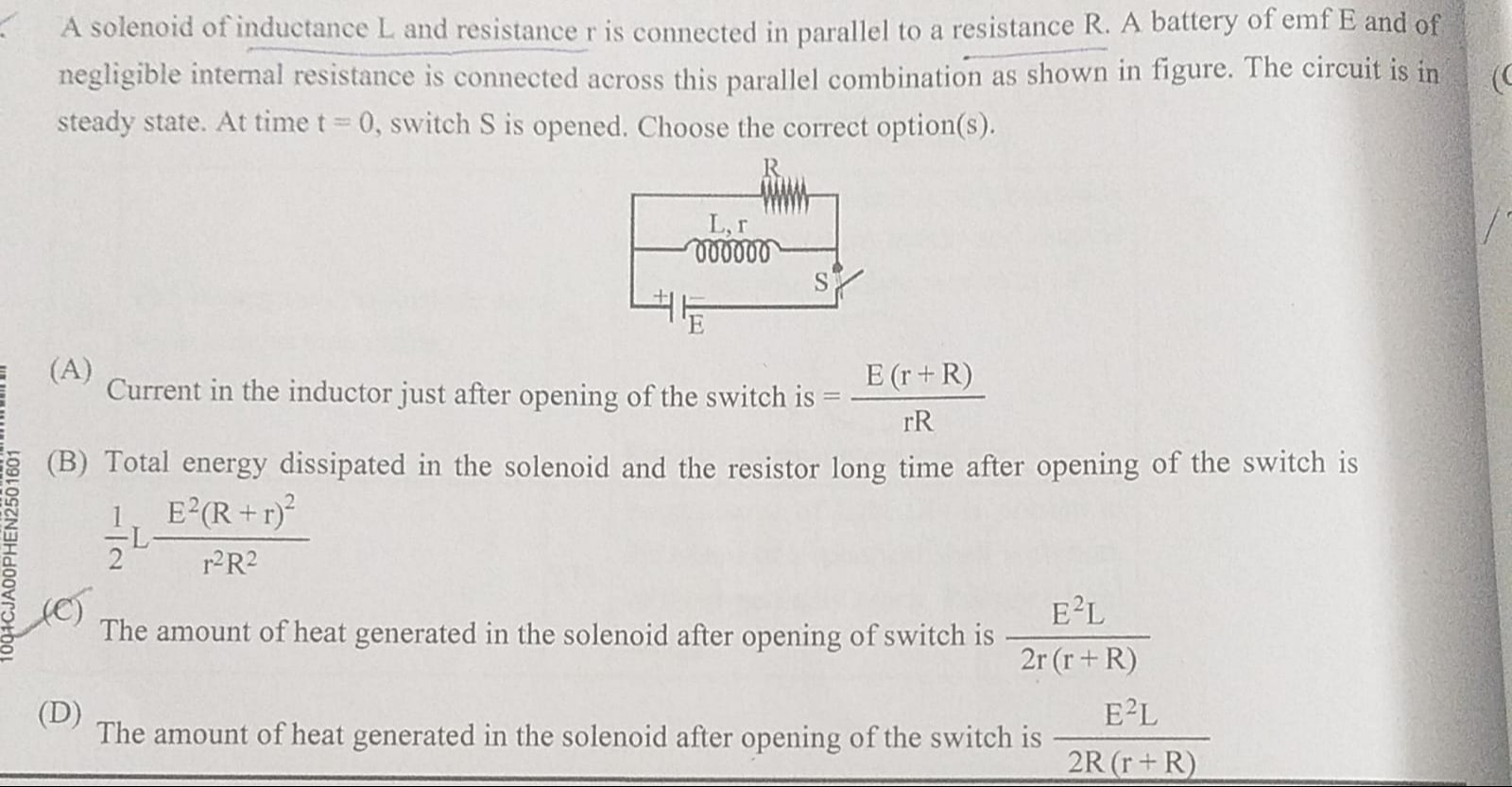
• A. Current in the inductor just after opening of the switch is = $\frac{E(r+R)}{rR}$
• B. Total energy dissipated in the solenoid and the resistor long time after opening of the switch is $\frac{1}{2}L\frac{E^2(R+r)^2}{r^2R^2}$
• C. The amount of heat generated in the solenoid after opening of switch is $\frac{E^2L}{2r(r+R)}$
• D. The amount of heat generated in the solenoid after opening of the switch is $\frac{E^2L}{2R(r+R)}$

Answer 1

Answer: (C)

C

Answer 2

In steady state, the inductor acts as a pure resistance $r$. The current through the inductor is $I_L = \frac{E}{r}$. When the switch is opened at $t=0$, the current through the inductor cannot change instantaneously. So, the current in the inductor just after opening the switch is $I_L(0^+) = \frac{E}{r}$. This makes option (A) incorrect.

After the switch is opened, the inductor discharges through the resistor $R$. The current in the inductor decays as $I_L(t) = \frac{E}{r} e^{-\frac{(r+R)t}{L}}$. The initial energy stored in the inductor is $U_0 = \frac{1}{2} L I_L(0^+)^2 = \frac{1}{2} L \left(\frac{E}{r}\right)^2 = \frac{1}{2} L \frac{E^2}{r^2}$. This is the total energy dissipated. Option (B) is incorrect.

The heat generated in the solenoid is given by: $H_{solenoid} = \int_0^\infty I_L(t)^2 r dt = \int_0^\infty \left(\frac{E}{r} e^{-\frac{(r+R)t}{L}}\right)^2 r dt$ $H_{solenoid} = \frac{E^2}{r} \int_0^\infty e^{-\frac{2(r+R)t}{L}} dt = \frac{E^2}{r} \left[-\frac{L}{2(r+R)} e^{-\frac{2(r+R)t}{L}}\right]_0^\infty$ $H_{solenoid} = \frac{E^2}{r} \left(0 - (-\frac{L}{2(r+R)})\right) = \frac{E^2 L}{2r(r+R)}$. This matches option (C). Option (D) is incorrect.