Question

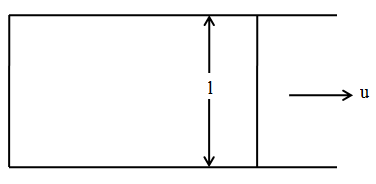
A soap film is created in a small wire frame as shown in the figure. The sliding wire of mass m is given a velocity u to the right. Assume that u is small enough so that film does not break. Plane of the film is horizontal and surface tension is T. Then time to regain the original position of wire is equal to:

A. $\dfrac{{um}}{{Tl}}$
B. $\dfrac{{Tl}}{{um}}$
C. ${\dfrac{{mu}}{{Tl}}^2}$
D. It will never regain original position

Answer 1

Calculate the total force acting on the sliding wire due to both surface films of the soap bubble. Use a kinematic equation to calculate the time taken by the sliding wire to go to the extreme right position. Twice of this time is the time taken by the sliding wire to regain its original position.

Formula used:
$v = u + at$
Here, v is the final velocity, u is the initial velocity, a is the acceleration and t is the time.

Complete step by step answer:
We see there are two films formed due to surface tension on the wire frame. Therefore, we can express the force on the sliding wire as,
$F = 2\left( {Tl} \right)$
Here, T is the tension and l is the length of the sliding wire.
Using Newton’s second law of motion, we can write,
$ma = 2\left( {Tl} \right)$
$\Rightarrow a = \dfrac{{2Tl}}{m}$ …… (1)
We can calculate the time required for sliding wire to go to extreme right as follows,
$v = u + at$
At an extreme position, the velocity of the sliding wire will become zero. Therefore, we can write the above equation as,
$0 = u - at$
$\Rightarrow u = at$
$\Rightarrow t = \dfrac{u}{a}$
The negative sign for acceleration implies that the velocity of the sliding wire is decreasing.
Using equation (1), we can rewrite the above equation as,
$t = \dfrac{u}{{\dfrac{{2Tl}}{m}}}$
$\Rightarrow t = \dfrac{{mu}}{{2Tl}}$
Now, we know that the time required to regain its original position is twice the above time. Therefore, the time required to regain the original position is,
$T = 2t = \dfrac{{mu}}{{Tl}}$

So, the correct answer is option (A).

Note:
Students should always consider the two surfaces of the soap film to determine the force. The soap bubble has two surfaces: inner surface and outer surface. Therefore, the tension force is doubled. Note that in this question, the time required to regain the original position is twice the time required to go to the extreme right position.