Question

A soap bubble with a radius ‘r’ is placed on another bubble with a radius R. Angles between the films at the points of contact will be.

A. $120^\circ$
B. $30^\circ$
C. $45^\circ$
D. $90^\circ$

Answer 1

Determine the force of surface tension along the tangents of the soap bubbles. Use Lami’s theorem to determine the angle of contact between the films at the point of contact.

Formula used:
The expression for Lami’s theorem is
$\dfrac{{{F_1}}}{{\sin \alpha }} = \dfrac{{{F_2}}}{{\sin \beta }} = \dfrac{{{F_3}}}{{\sin \gamma }}$
Here, $\alpha$ is the angle made by forces ${F_1}$ and ${F_2}$, $\beta$ is the angle made by the forces ${F_2}$ and ${F_3}$ and $\gamma$ is the angle made by the forces ${F_3}$ and ${F_1}$.

Complete step by step answer:
The soap bubble with a radius ‘r’ is placed on another bubble with a radius R.
Draw the diagram of the soap bubbles with the tension force on them.

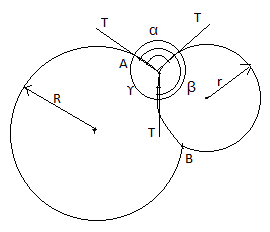
The two soap bubbles are stable when placed on each other means they are in equilibrium and hence the surface tension force $T$ acting along the tangent on both the soap bubbles is the same.
In the diagram, $\alpha$, $\beta$ and $\gamma$ are the three angles made by the tangents to the soap bubbles.
The angle of contact between the two soap bubbles is made by the tangents to the bubble.
According to Lami's theorem, the sine of angle between the remaining two forces is proportional to the force provided the three forces are in equilibrium.
Apply Lami’s theorem to the three surface tension forces along the tangents.
$\dfrac{T}{{\sin \alpha }} = \dfrac{T}{{\sin \beta }} = \dfrac{T}{{\sin \gamma }}$
$\Rightarrow \sin \alpha = \sin \beta = \sin \gamma$
$\Rightarrow \alpha = \beta = \gamma$
The sum of all the angles at a point in a three-dimensional space is $360^\circ$.
$\alpha + \beta + \gamma = 360^\circ$
Substitute $\alpha$ for $\beta$and $\gamma$ in the above equation.
$\alpha + \alpha + \alpha = 360^\circ$
$\Rightarrow 3\alpha = 360^\circ$
$\Rightarrow \alpha = 120^\circ$
$\alpha = \beta = \gamma = 120^\circ$
Therefore, the angle of contact between the films at the point of contact is $120^\circ$.

So, the correct answer is “Option A”.

Note:
Since the soap bubbles are in equilibrium, the angles $\alpha$, $\beta$ and $\gamma$ must be the same.
The two soap bubbles are stable when placed on each other means they are in equilibrium.