Question

A soap bubble of radius 2 cm is formed in another soap bubble of radius 6 cm.
Minimum possible radius with the pressure of this case is
A. $\dfrac{5}{3}\,{\text{cm}}$
B. $\dfrac{7}{3}\,{\text{cm}}$
C. $\dfrac{4}{3}\,{\text{cm}}$
D. $\dfrac{3}{2}\,{\text{cm}}$

Answer 1

The excess pressures inside each bubble will exert a pressure on one another. Recall the expression for the excess pressure inside a bubble and express it for both the bubbles. The net excess pressure will be the sum of the excess pressure inside both the bubbles.

Formula used:
Excess pressure, $P = \dfrac{{4T}}{r}$

Here, T is the surface tension and $r$ is the radius of the soap bubble.

Complete step by step answer:

We have given the two soap bubbles such that one soap bubble of radius 2 cm is formed
inside the soap bubble of radius 6 cm. As we know, there is always an excess pressure inside
the soap bubble than the atmospheric pressure. These excess pressures inside each bubble
will exert a pressure on one another as shown in the figure below.

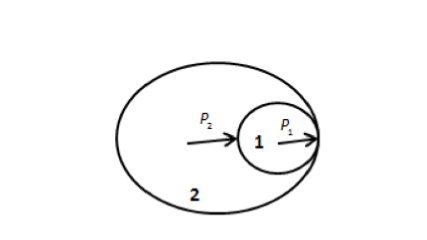
In the above figure, soap bubble 1 has excess pressure ${P_1}$ and soap bubble 2 has
excess pressure ${P_2}$.

Let’s express the excess pressure inside the smaller soap bubble as follows,
${P_1} = \dfrac{{4T}}{{{r_1}}}$ …… (1)

Here, T is the surface tension and ${r_1}$ is the radius of the smaller soap bubble.

Let’s express the excess pressure inside the larger soap bubble as follows,
${P_2} = \dfrac{{4T}}{{{r_2}}}$ …… (2)

Here, ${r_2}$ is the radius of the larger soap bubble.

The net excess pressure in this case will be,
$P = {P_1} + {P_2}$
$\Rightarrow \dfrac{{4T}}{r} = \dfrac{{4T}}{{{r_1}}} + \dfrac{{4T}}{{{r_2}}}$
$\Rightarrow \dfrac{1}{r} = \dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}}$

Substituting ${r_1} = 2\,{\text{cm}}$ and ${r_2} = 6\,{\text{cm}}$ in the above equation,
we get,
$\dfrac{1}{r} = \dfrac{1}{2} + \dfrac{1}{6}$
$\Rightarrow \dfrac{1}{r} = \dfrac{2}{3}$
$\Rightarrow r = \dfrac{3}{2}\,{\text{cm}}$

So, the correct answer is option (D).

Note: Note that the surface tension will be the same for both the soap bubbles. The smaller soap bubble will always be attached to the inner wall of the larger soap bubble. In this way, the larger soap bubble will exert a pressure on the smaller bubble. The pressure inside the soap bubble is always greater than the outside atmospheric pressure.