Question

A soap bubble is formed from $5\times {{10}^{-3}}g$ of soap solution. When filled with hydrogen of density $0.0009g/c{{m}^{3}}$, it floats in air of density of $0.00129g/c{{m}^{3}}$. If surface tension of soap solution is $30dyne/cm$, the excess pressure in $dyne/c{{m}^{2}}$is:
(A) 30
(B) 60
(C) 120
(D) 240

Answer 1

The tricky part in questions where a lot of different data is given to us is to find out where to start solving from. We know the mass of the soap solution and it’s filled with hydrogen whose density has been given to us, so we can find the volume of our bubble and from the obtained volume, we can find the radius of the bubble and use the formula for excess pressure. We have also been given that our bubble floats in air, which means we’ll have to consider the buoyant force of air on the bubble. So let’s dive right in and start solving this bad boy.

Complete step by step answer:

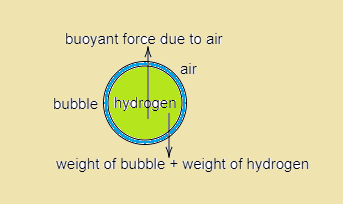
As we can see clearly the different forces acting on our bubble, we’ll form the balanced weight equation for our bubble,
Let the volume of our bubble be V cm3
Weight of bubble + weight of hydrogen = buoyant force due to air

& 5\times {{10}^{-3}}g+0.0009\times V\times g=0.00129\times V\times g \\\ & 0.00039V=0.005g \\\ & V=\dfrac{0.005}{0.00039}=12.82 c{{m}^{3}} \\\ \end{aligned}$$ Since our bubble is a sphere of radius r (let’s assume), volume of our bubble, $$V=\dfrac{4}{3}\pi {{r}^{3}}$$ Hence, radius(r) = $${{\left( \dfrac{3V}{4\pi } \right)}^{1/3}}=0.998cm\simeq 1cm$$ Now we know that excess pressure in a soap bubble is 4T/r Hence, excess pressure, P = $$\dfrac{4\times 30dyne/cm}{1cm}=120 dyne/c{{m}^{2}}$$ **Note:** normally we used the formula excess pressure = 2T/r in case of water drops, but what we have to be aware of here is that we have been given a bubble. Now a bubble has two free surfaces, so the excess pressure becomes twice, once for the outer surface, once for the inner surface, hence we used the formula excess pressure P = 4T/r. We always have to be aware of such minute technicalities of the question as these are the examiner’s weapons.