Question

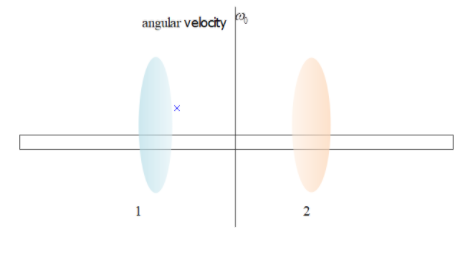
A smooth uniform rod of length l and mass m has two identical beads of negligible size, each of mass m, which can slide freely along the rod. Initially, the two beads are at the centre of the rod and the system is rotating with an angular velocity ${{\omega }_{0}}$​ about an axis perpendicular to the rod and passing through the midpoint of the rod (see figure). There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is

Answer 1

When the two given beads each of mass m are at the centre of the rod, calculate the moment of inertia of the beads. Next, at the final position, when they are at the end of the rod, calculate the moment of inertia. As there’s no external force acting on the system, the net angular momentum is conserved for the beads.

Formulas used:
$J=I{{\omega }_{{}}}$

Complete answer:
Let us assume the angular momentum of the beads before and after the change in the position of the beads as ${{J}_{in}},{{J}_{f}}$ respectively. Now, let’s first calculate the moment of inertia of the beads when they are present at the centre of the rod.
$I=\dfrac{M{{L}^{2}}}{12}$ when they are at the centre of the rod.
After moving, they move to the end of the rod.
At the end of the rod, the moment of inertia will be equal to
$\begin{aligned} & I=(\dfrac{M{{L}^{2}}}{12}+2m{{(\dfrac{L}{2})}^{2}}) \\\ & \\\ \end{aligned}$
As there’s no external force acting on the system, the net angular momentum is conserved.
I.e.
$\begin{aligned} & {{J}_{in}}={{J}_{f}} \\\ & \dfrac{M{{L}^{2}}}{12}{{\omega }_{0}}=I=(\dfrac{M{{L}^{2}}}{12}+2m{{(\dfrac{L}{2})}^{2}})\omega \\\ & \Rightarrow \dfrac{M}{12}{{\omega }_{0}}=(\dfrac{M}{12}+\dfrac{m}{2})\omega \\\ & \Rightarrow \omega =\dfrac{M{{\omega }_{0}}}{M+6m} \\\ \end{aligned}$
There, the above is the angular acceleration of the system when the beads reach the ends of the rod.

Additional information:
Angular momentum is equivalent to the rotational linear momentum. Angular momentum is conserved quantity. The total angular momentum of a system when no external force is acting on it is always conserved. There are two types of angular momentums. One is spin angular momentum and the other is orbital angular momentum. Spin angular momentum is the angular momentum about the object's centre of mass coordinate. The orbital angular momentum is the angular momentum of the object about a chosen origin. We can say, the total angular momentum as the sum of the spin and orbital angular momentum. Orbital angular momentum is always parallel and directly proportional to the angular velocity. Spin sometimes is parallel and sometimes not.

Note:
During the calculation of the final moment of inertia of the particles, the net mass is taken as twice the mass as two beads are present. The distance travelled by each of the beads is half the length, therefore the distance travelled is half of the length of the rod and the mass of the beads is the total mass of the beads.