Question

A smooth track in the form of a quarter circle of radius $6\,m$ lies in a vertical plane. A particle moves from ${P_1}$ to ${P_2}$ undergo the forces $\overrightarrow {{F_1}}$, $\overrightarrow {{F_2}}$,$\overrightarrow {{F_3}}$. Force $\overrightarrow {{F_1}}$ is always towards ${P_2}$ and is always $20\,N$ in magnitude, force $\overrightarrow {{F_2}}$ always acts tangentially and it is always $15\,N$ in magnitude. Force $\overrightarrow {{F_3}}$ always acts horizontally is of magnitude $30\,N$. Select the correct alternative(s):

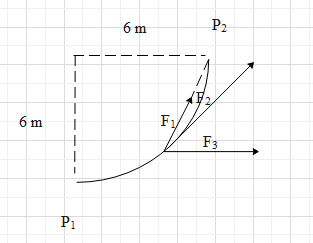
A. work done by $\overrightarrow {{F_1}}$ is $120J$
B. work done by $\overrightarrow {{F_2}}$ is $45\pi J$
C. work done by $\overrightarrow {{F_3}}$ is $180\,J$
D. $\overrightarrow {{F_1}}$ is conservative in nature.

Answer 1

Hint-
Work done is the product of force and displacement of force in the direction of force.
Work is represented in equation form as

In the case of ${F_1}$

Here, $ds$ which is the displacement in the direction of $\overrightarrow {{F_1}}$ is the distance from ${P_{1\,}}$ to ${P_2}$.
In the case of ${F_2}$
Work done by ${F_2}$ is along the arc ${P_1}{P_2}$
${W_{{F_2}}} = \int {{F_2}} ds$
Given arc is a quarter of a full circle.
Therefore, arc length is circumference of the circle divided by 4.
In case of ${F_3}$

Here displacement along direction of ${F_3}$ is the horizontal displacement which is $6\,m$
A force is said to be conservative, if the work done by it is path independent.

Complete step-by-step answer:
Work done is the product of force and displacement of force in the direction of force.
Work is represented in equation form as

In the case of ${F_1}$

Given${F_1} = 20N$
$ds$ which is the displacement in the direction of $\overrightarrow {{F_1}}$ is the distance from ${P_{1\,}}$ to ${P_2}$.
Using Pythagoras theorem, we get distance of line
${P_1}{P_2} = \sqrt {{6^2} + {6^2}\,}$
${P_1}{P_2} = 6\sqrt 2$
Substituting the given values, we get,
${W_{{F_1}}} = 20N \times 6\sqrt 2 = 120\sqrt 2 J$
In the case of ${F_2}$
Work done by ${F_2}$ is along the arc ${P_1}{P_2}$
${W_{{F_2}}} = \int {{F_2}} ds$
Given arc is a quarter of a full circle.
Therefore, arc length is circumference of the circle divided by 4.
${p_1}{p_2} = \dfrac{{2\pi r}}{4} = \dfrac{{\pi r}}{2}$
${W_{{F_2}}} = 15 \times \dfrac{{\pi r}}{2} \\\ = 15 \times \pi \times \dfrac{6}{2} \\\ = 45\pi J \\\$
In case of ${F_3}$

Here displacement along direction of ${F_3}$ is the horizontal displacement which is $6\,m$

$${W_{{F_3}}} = 30 \times 6 \\\ = 180J \\\$$

Now a force is said to be conservative, if the work done by it is path independent. Since work done by $\overrightarrow {{F_1}}$ depends only on initial and final position, we can say that ${F_1}$ is conservation.

So, the correct options are option B, C and D

Note: Remember that while calculating work the force should be multiplied by the displacement in the direction of force. In each cases of work for forces $\overrightarrow {{F_1}}$, $\overrightarrow {{F_2}}$, $\overrightarrow {{F_3}}$ the displacement will differ according to the direction of these forces. So, in each case consider the component of displacement in the direction of corresponding force.