Question

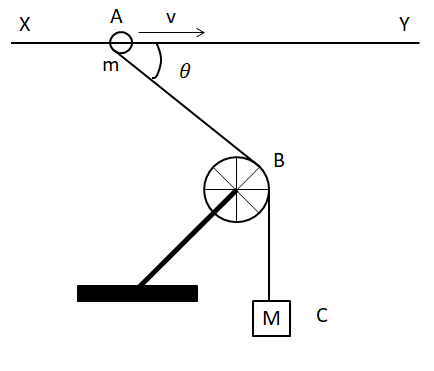
A smooth ring A of mass m can slide on a fixed horizontal rod XY. A string tied to the ring passes over a fixed pulley B and carries a block C of mass M(=2m) as shown in the figure below. At an instant the string between the ring and pulley makes an angle $\theta$ with the rod.
a. Show that if the ring slides with velocity v, the block descends with speed $v\cos \theta$.
b. With what acceleration will the ring start moving if the system is released from rest with $\theta ={{30}^{0}}$?

Answer 1

Hint: Newton’s laws of motion are required to solve this problem. Making free body diagrams and taking approximations where ever required will solve the two cases. For the first case, consider the ring to have moved a distance in some time dt and making a diagram of the system after the time will solve the problem. Similarly, for the second case, making an individual force body diagram for both the mass M and the ring will help in solving the problem.

Step by step solution:
From the problem we have, the initial position of the ring of mass m to be at A and the pulley at B and the mass M=2m at point C.
For the first case, let’s consider the ring to have moved to a new position ${A}'$. Due to this, the mass M will have moved to a new position ${C}'$. Since the string connecting the ring through the pulley to the mass M is inextensible and mass less, hence the net length of the string will remain the same. Let’s drop a perpendicular from the position ${A}'$ to the length AB at position P. Below is a diagram of the system.

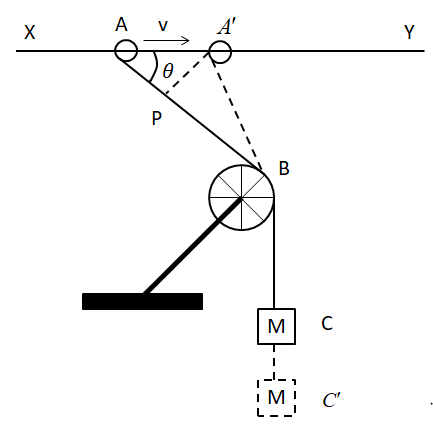
Since, the length of the string is the same. Hence, the length $AB+BC={A}'B+B{C}'$.
This becomes, $AP+PB+BC={A}'B+BC+C{C}'$. However, $PB\approx {A}'B$, since the perpendicular is dropped from the position ${A}'$.
Hence, $AP+PB+BC={A}'B+BC+C{C}'\Rightarrow AP=C{C}'$. From the right angled triangle of $A{A}'P$, we get $\Rightarrow A{A}'\cos \theta =C{C}'$, dividing the whole equation with the time interval, we get, $\dfrac{A{A}'}{dt}\cos \theta =\dfrac{C{C}'}{dt}$. Since, we know that the velocity of the ring is v, therefore the above relation becomes, $v\cos \theta =\dfrac{C{C}'}{dt}\Rightarrow {v}'=v\cos \theta$, where ${v}'$is the velocity with which the mass M descends. Hence, we find that ${v}'=v\cos \theta$.
For the second case, we will consider the force body diagram for both the mass M and the ring.
The force body diagram of the system is below.

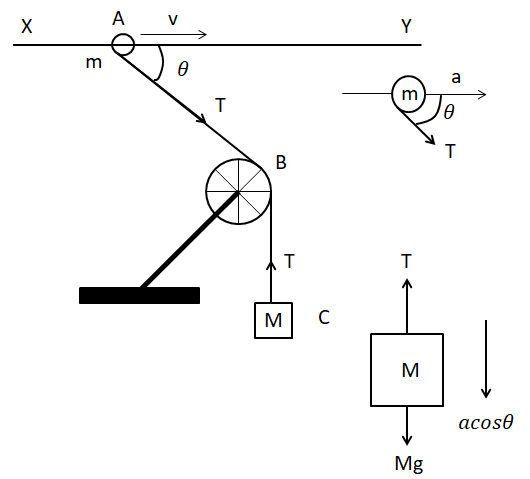
For the body of mass M, we find that the force Mg is acting downwards and an equal amount of tension T acting in the upward direction. The net acceleration of the body is given by $a\cos \theta$.
Hence, equating the net force acting on the body is given by, $Mg-T=M(a\cos \theta )\Rightarrow 2mg-T=2ma\cos \theta \to (1)$.
Similarly, for the ring of mass m, having an acceleration a and tension T pulling the ring, we can equate the forces as, $ma=T\cos \theta \to (2)$.
From eqn.(1) and eqn.(2) we get, $2mg-T=2ma\cos \theta \Rightarrow 2mg-\dfrac{ma}{\cos \theta }=2ma\cos \theta \Rightarrow 2g=2a\cos \theta +\dfrac{a}{\cos \theta }$.
Given in the question, the angle $\theta ={{30}^{0}}$. Substituting in this value in the equation above, we get, $2g=(\dfrac{2{{\cos }^{2}}\theta +1}{\cos \theta })a\Rightarrow a=\dfrac{2g\cos \theta }{2{{\cos }^{2}}\theta +1}=\dfrac{2g(\dfrac{\sqrt{3}}{2})}{2{{(\dfrac{\sqrt{3}}{2})}^{2}}+1}=\dfrac{\sqrt{3}g}{\dfrac{3}{2}+1}\Rightarrow a=\dfrac{2\sqrt{3}g}{5}$.
Hence, the acceleration of the ring for $\theta ={{30}^{0}}$is $a=\dfrac{2\sqrt{3}g}{5}$.

Note: We need to understand that the approximation in the first case for $PB\approx {A}'B$ is only possible when the displacement is very small. Whenever, a perpendicular is dropped from two lines emerging from the common point, for very small angle in between the two angles, the distances will be equal for distance at the center to the point where perpendicular is dropped and the distance from the center to the point from where the perpendicular is dropped.