Question
Question: A smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the rod passes over ...
A smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the rod passes over a fixed pulley B and carries a block C of mass 2m as shown in the figure. At the instant the string between the ring and the pulley makes an angle θ with the rod. With what acceleration will the ring start moving if the system is released from rest with θ=600.
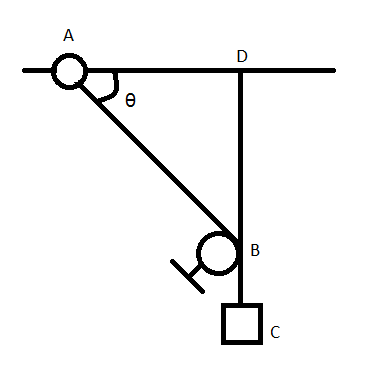
A) 32g
B) 3g
C) 2g
D) 23g
Solution
Hint: This problem can be solved by first deriving a relation between the instantaneous velocities of the ring and the block in terms of θ and each other. Then this relation can be used to find out the relation between the instantaneous accelerations of the ring and the block.
This relation can be applied after finding the value of the acceleration of the block and the ring by using the free body diagrams of both bodies and finding out the acceleration of each.
Formula used:
instantaneous velocity = time !!Δ!! displacement
instantaneous acceleration = time !!Δ!! velocity
F=ma
Where F is the force applied on or by a body, m is the mass and a is the acceleration of the body due to that force.
Complete step-by-step answer:
We will first use geometry of the figure to find out the relation between the instantaneous displacements of the ring and the block.
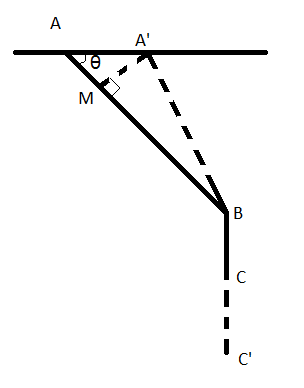
Let the ring move a small distance AA’ and the block moves a distance CC’.
Now, since the string is considered to be inextensible, the total length of the string does not change.
AB+BC=A′B+BC′
⇒AM+MB+BC=A′B+BC′ --(1)
Now, since AA’ is very small, A′B≈MB --(2)
Putting (2) in (1),
AM+BC=BC′
⇒AM=BC′−BC
⇒AA′cosθ=BC′−BC
⇒displacement of ring×cosθ = displacement of block --(3)
Now, instantaneous velocity = time !!Δ!! displacement --(4)
instantaneous acceleration = time !!Δ!! velocity--(5)
Dividing (3) by time,
⇒timedisplacement of ring×cosθ = timedisplacement of block
Using (4),
⇒velocity of ring×cosθ = velocity of block--(6)
Dividing (6) by time,
⇒timevelocity of ring×cosθ = timevelocity of block
Using (5),
⇒acceleration of ring×cosθ = acceleration of block
⇒aringcosθ=ablock --(7)
where aring and ablockare the instantaneous accelerations of the ring and the block respectively.
Now, drawing the free body diagram of the block,
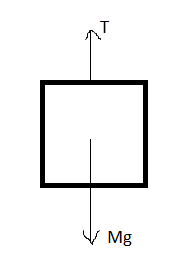
Where M=2m is the mass of the block and m is the mass of the ring and T is the tension of the string.
Using, F=ma
Mg−T=Mablock
T=Mg−Mablock --(8)
Now drawing the free body diagram of ring,
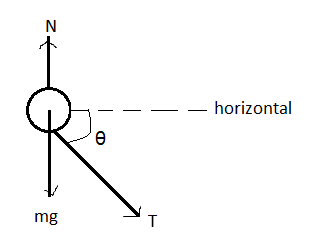
Where N is the normal force due to the rod, T is the tension due to the string and mg is its weight.
Applying F=ma in the horizontal direction,
Tcosθ=maring --(9)
Putting (8) and (7) in (9),
(Mg−Maringcosθ)cosθ=maring --(10)
Now, given M=2m --(11)
Putting (11) in (10),
2m(g−aringcosθ)cosθ=maring
⇒2gcosθ−2aringcos2θ=aring
⇒aring(2cos2θ+1)=2gcosθ
⇒aring=2cos2θ+12gcosθ --(12)
According to the question, θ=600. Putting this value in (12),
aring=2×(0.5)2+12g×0.5=0.5+1g=1.5g=32g
Hence, the acceleration of the ring is 32g .
Therefore the correct option is A) 32g.
Note: The correct way to solve such questions is to apply geometry as shown above and to first derive a relation between different physical quantities by using geometry. Since, these problems are not very intuitive in nature. In fact, using intuition in such questions can lead to a wrong thinking process and in turn lead to a silly mistake.
Intuition might lead to think that at first glance the acceleration of the ring is the acceleration of the block multiplied by cosθ, however, as seen above, it is actually the absolute other way round.
