Question

A smooth block is released at rest on a $45{}^\circ$ incline and then slides a distance $d$ . The time taken to slide is $n$ times as much to slide on a rough incline as on a smooth incline. The coefficient of friction is
(A) ${{\mu }_{k}}=\sqrt{1-\dfrac{1}{{{n}^{2}}}}$
(B) ${{\mu }_{k}}=1-\dfrac{1}{{{n}^{2}}}$
(C) ${{\mu }_{s}}=\sqrt{1-\dfrac{1}{{{n}^{2}}}}$
(D) ${{\mu }_{s}}=1-\dfrac{1}{{{n}^{2}}}$

Answer 1

Hint : Here we are given distance traveled by the block, time taken to travel, acceleration of the block, and initial velocity of the block. Hence, using the equation of uniform accelerated motion $s=ut+\dfrac{1}{2}a{{t}^{2}}$ . From the equation, we can find the time taken and then find the relation between the time taken for both cases.

Complete Step By Step Answer:
Let us note down the given data,
Here, we are given an initially stationary object $\Rightarrow u=0m{{s}^{-1}}$
The object is lying on an inclined plane at an angle $\theta =45{}^\circ$
The object travels a distance $d$ in the time $t$
As the plane is smooth, there is no frictional force acting on it.
Hence, the acceleration of the object is only due to the gravitational force.
We know that the gravitational force on the object acts vertically down. But here as the object is on an inclined plane, we need to find the component of the gravitational force in the direction of movement of the block as shown in the figure

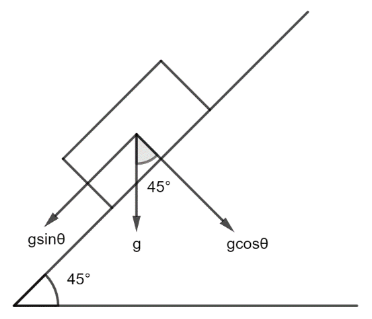
From the above figure, we can conclude that acceleration acting in the direction of sliding of the block is $a=g\sin \theta$
Now, as we have all the values required, we can substitute the values in the equation to find the distance for uniformly accelerated motion i.e. $s=ut+\dfrac{1}{2}a{{t}^{2}}$
Substituting the values,
$\therefore d=(0)t+\dfrac{1}{2}(g\sin \theta ){{t}^{2}}$
$\therefore d=\dfrac{1}{2}(g\sin \theta ){{t}^{2}}$
Rearranging the equation to make time the subject of the equation.
$\therefore$ Time required by block to move on smooth plane ${{t}_{s}}=\sqrt{\dfrac{2d}{g\sin \theta }}$ …… $(1)$
Now, if the plane is rough, the object will encounter deceleration due to frictional force $F$ in the opposite direction of its motion.
We know that acceleration due to normal force $N$ acts on the object in a vertically upward direction as shown in the figure,

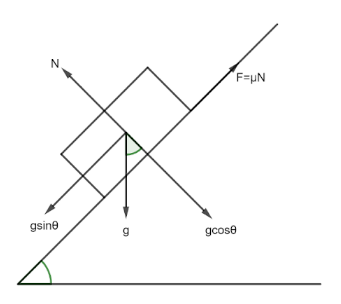
As there is no motion in the vertical direction, from the geometry of the figure we can write
$N=g\cos \theta$
Here, we have considered the body of unit mass
Now, substituting this value in the formula of frictional force.
$\therefore F={{\mu }_{k}}(g\cos \theta )$
Now this force acts opposite to the gravitational force,
Hence, for the unit mass, the effective acceleration is given as,
$a=g\sin \theta -{{\mu }_{k}}g\cos \theta$
Now, substituting this value in the equation of uniformly accelerated motion,
$\therefore d=(0)t+\dfrac{1}{2}(g\sin \theta -{{\mu }_{k}}g\cos \theta ){{t}^{2}}$
$\therefore d=\dfrac{1}{2}(g\sin \theta -{{\mu }_{k}}g\cos \theta ){{t}^{2}}$
Rearranging the equation to make time the subject of the equation.
$\therefore$ Time required by block to move on rough plane ${{t}_{r}}=\sqrt{\dfrac{2d}{g\sin \theta -{{\mu }_{k}}g\cos \theta }}$ …… $(2)$
Now, we are given that time taken to move on a rough plane is $n$ times of time taken to move on a smooth plane.
$\therefore {{t}_{r}}=n{{t}_{s}}$
Substituting the derived equations,
$\therefore \sqrt{\dfrac{2d}{g\sin \theta -{{\mu }_{k}}g\cos \theta }}=n\sqrt{\dfrac{2d}{g\sin \theta }}$
Squaring on both sides,
$\therefore \dfrac{2d}{g\sin \theta -{{\mu }_{k}}g\cos \theta }={{n}^{2}}\dfrac{2d}{g\sin \theta }$
Removing the common part,
$\therefore \dfrac{1}{g\sin \theta -{{\mu }_{k}}g\cos \theta }={{n}^{2}}\dfrac{1}{g\sin \theta }$
Applying cross multiplication,
$g\sin \theta ={{n}^{2}}(g\sin \theta -{{\mu }_{k}}g\cos \theta )$
Removing the common part and putting the value of the angle,
$\therefore \sin 45{}^\circ ={{n}^{2}}(\sin 45{}^\circ -{{\mu }_{k}}\cos 45{}^\circ )$
$\therefore \dfrac{1}{\sqrt{2}}={{n}^{2}}\left( \dfrac{1}{\sqrt{2}}-{{\mu }_{k}}\dfrac{1}{\sqrt{2}} \right)$
Canceling the common part,
$\therefore 1={{n}^{2}}\left( 1-{{\mu }_{k}} \right)$
$\therefore 1={{n}^{2}}-{{n}^{2}}{{\mu }_{k}}$
Rearranging equation to make coefficient of friction as the subject of the equation
$\therefore {{n}^{2}}{{\mu }_{k}}={{n}^{2}}-1$
$\therefore {{\mu }_{k}}=\dfrac{{{n}^{2}}-1}{{{n}^{2}}}$
Hence, we get the coefficient of friction as,
$\therefore {{\mu }_{k}}=1-\dfrac{1}{{{n}^{2}}}$
Hence, the correct answer is Option $(B)$ .

Note :
Here as we are concerned with the acceleration of the block, to obtain the equation in the form of acceleration we have considered the object to be of unit mass. If a mass is mentioned, we must include it in the equation of force. However, we can see from the final answer that coefficient does not depend on the mass.