Question

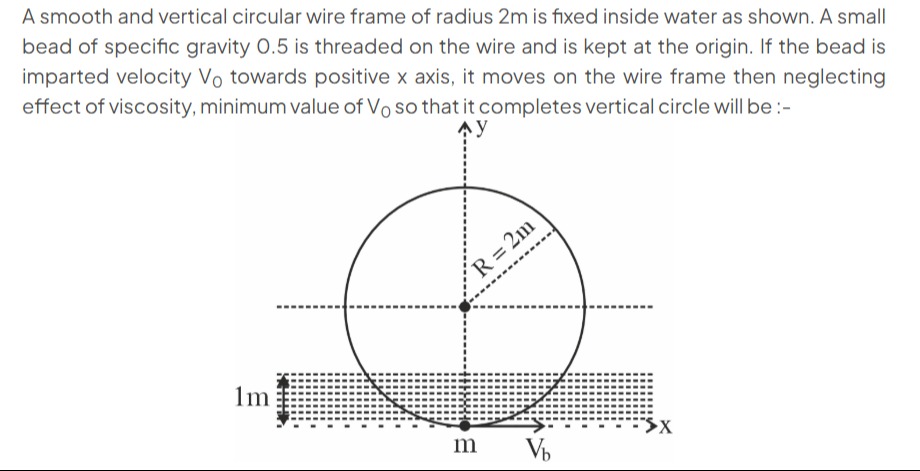
A smooth and vertical circular wire frame of radius 2m is fixed inside water as shown. A small bead of specific gravity 0.5 is threaded on the wire and is kept at the origin. If the bead is imparted velocity $V_0$ towards positive x axis, it moves on the wire frame then neglecting effect of viscosity, minimum value of $V_0$ so that it completes vertical circle will be :-

Answer 1

V_0=\sqrt{6g}

Answer 2

Solution:

1. Setup and Forces:
   A bead of density 0.5 (ρ_water) has mass

   $$m=0.5\,\rho\,V.$$

   Its weight is

   $$W = m g =0.5\rho V\,g,$$

   while the buoyant force is

   $$F_B = \rho V\,g.$$

   Thus, when completely submerged the net force is upward:

   $$F_{\rm net}= F_B - W = \rho V\,g-0.5\,\rho V\,g =0.5\,\rho V\,g = m g.$$

   That is, underwater the bead “feels” a constant upward force $= m g$. In air (above water) it feels the usual weight $m\,g$ downward.

2. Assigning Potential Energies:
   Place the reference $y=0$ at the bottom of the circle where the bead starts (which is underwater, since the water level is $y=1$ m).

   • For the underwater portion ($y\le1$), the net force is upward ($m\,g$ upward), so we take $$U_{\rm water}(y)=-mgy.$$
   • For the part in air ($y>1$), the force is downward ($m\,g$ downward) so we choose $$U_{\rm air}(y)=mgy+C.$$ Continuity at $y=1$ requires: $$-mg = m g(1) + C\quad\Longrightarrow\quad C=-2mg.$$ Thus, for $y>1$ $$U_{\rm air}(y)= mgy- 2mg.$$

3. Energy Considerations Along the Circular Path:
   The circle has radius $R=2$ m, with its bottom at $y=0$ and top at $y=4$. The bead starts at the bottom ($y=0$) with kinetic energy

   $$K_0=\tfrac{1}{2}mV_0^2,$$

   and potential $U(y=0)=0$.

   At the top ($y=4$) the potential energy is (using the air expression):

   $$U_{\rm top}= mg(4)-2mg=2mg.$$

   For the bead to remain in contact with the wire at the top, the minimum speed $v_{\rm top}$ must satisfy the condition that the centripetal force is provided by weight:

   $$\frac{mv_{\rm top}^2}{R}= mg\quad\Longrightarrow\quad v_{\rm top}=\sqrt{gR}=\sqrt{2g}.$$

   Hence, the kinetic energy at the top must be at least

   $$K_{\rm top}=\tfrac{1}{2}m(2g)= mg.$$

4. Energy Conservation (piecewise but continuous):
   Total energy at bottom equals that at the top:

   $$\tfrac{1}{2}mV_0^2 = U_{\rm top}+K_{\rm top} = 2mg + mg = 3mg.$$

   Therefore, the minimum initial speed is

   $$V_0=\sqrt{6g}.$$

Explanation (minimal):

• Underwater, the bead’s effective force is upward $= m\,g$ giving potential $U=-mgy$; in air, $U=mgy-2mg$.
• The total energy needed to go from $y=0$ to $y=4$ is an increase of $2mg$ in potential energy, plus at the top the bead must have kinetic energy $mg$ (since $v_{\rm top}=\sqrt{2g}$ from $mv^2/R=mg$).
• Energy conservation gives $\tfrac{1}{2}mV_0^2=3mg$, leading to $V_0=\sqrt{6g}$.