Question

A small wooden ball of density $\rho$ is immersed in water of density $\sigma$ to depth $h$ and then released. The height $H$ above the surface of water up to which the ball will jump out of water is
(A) $\dfrac{{\sigma h}}{\rho }$
(B) $\left( {\dfrac{\sigma }{\rho } - 1} \right)h$
(C) $h$
(D) $zero$

Answer 1

Hint To solve this question, we need to consider the free body diagram of the ball when it is underwater. Then applying the work energy theorem and the energy conservation principle, we can find out the required maximum height of the ball.

Formula Used: The formula used to solve this question is given by
$\Rightarrow {F_B} = {V_i}\sigma g$ , here ${F_B}$ is the buoyant force acting on a body whose ${V_i}$ portion of the volume is immersed inside a fluid of density $\sigma$ .

Complete step by step answer
Let the volume of the ball be $V$ .
As we know that the wood is lighter than water, so the density of the wooden ball must be less than that of the water, which means
$\Rightarrow \rho < \sigma$
Due to this reason, the ball is coming out of the surface of water, and is not sinking into.
Now, an upward force is required to oppose the weight of the ball in order to make it jump out. This force is provided by the water as the buoyant force. Now, we consider the free body diagram of the ball at the depth $h$ , as shown below.

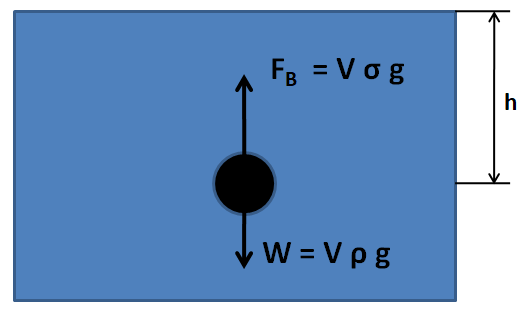
The forces acting on the ball are:
The weight of the block $\left( W \right)$ - The weight of a body is given by
$\Rightarrow W = mg$
The mass of the ball can be written in terms of its density as
$\Rightarrow m = V\rho$ ………………….(1)
$\therefore W = V\rho g$ ………………….(2)
The buoyant force $\left( {{F_B}} \right)$ - We know from the Archimedes’ principle that the buoyant force on a body immersed in a fluid is given by
$\Rightarrow {F_B} = {V_i}\sigma g$
As the ball is completely immersed inside the water so ${V_i} = V$ . Therefore the buoyant force on the ball is
$\Rightarrow {F_B} = V\sigma g$ ………………….(3)
When the ball is released from this point, it will begin to move upwards. So, the ball will start gaining kinetic energy, which was initially zero at the point when the ball was released. It will become maximum at the surface of water.
The net upward force on the ball during this journey is
$\Rightarrow F = {F_B} - W$
From (2) and (3)
$\Rightarrow F = V\sigma g - V\rho g$
$\Rightarrow F = V\left( {\sigma - \rho } \right)g$
By applying the work energy theorem, the kinetic energy at the surface of water is given by
$\Rightarrow K = Fh$
$\Rightarrow K = V\left( {\sigma - \rho } \right)gh$ …………………..(4)
This is the maximum kinetic energy of the ball, as after this point, there will be no upward buoyant force acting on the ball. The only external force on the ball will be its own weight. So, the total mechanical energy of the ball will be conserved. Thus, when the ball will reach its maximum height, the potential energy will become maximum, which will be equal to the maximum kinetic energy of the ball which is obtained above.
The potential energy of the block at the maximum height is given by
$\Rightarrow U = mgH$
From (2)
$\Rightarrow U = V\rho gH$ ………………………….(5)
As this is equal to the maximum kinetic energy, so from (4)
$\Rightarrow U = V\left( {\sigma - \rho } \right)gh$ ………………….(6)
Equating (5) and (6)
$\Rightarrow V\rho gH = V\left( {\sigma - \rho } \right)gh$
Cancelling $Vg$ from both the sides, we get
$\Rightarrow \rho H = \left( {\sigma - \rho } \right)h$
Finally we get the maximum height of the ball as
$\Rightarrow H = \dfrac{{\left( {\sigma - \rho } \right)}}{\rho }h$
$\therefore H = \left( {\dfrac{\sigma }{\rho } - 1} \right)h$
Hence the correct answer is option B.

Note
Do not worry about the radius of the ball in the calculations. As it is given in the question that the ball is small, so we can neglect its radius with respect to the depth and the maximum height. Hence the ball in this question is approximated to be a point object.