Question

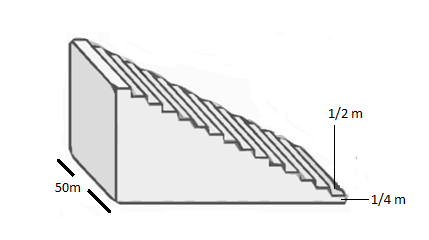
A small terrace at a football ground comprises 15 steps each of which is 50m long and built of solid concrete. Each step has a rise of $\dfrac{1}{4}m$ and a tread of $\dfrac{1}{2}m$. Calculate the total volume of concrete required to build the terrace.

Answer 1

We can divide the terrace as horizontal layers with each step with length and height the same and the width increasing as we go down. Then we can formulate the increasing width as an AP and find its sum. Then we can write the volume of the step as the series of volumes of each step. After taking the common terms, we are left with the sum of the breadth. After substitution and simplification, we can obtain the required volume.

Complete step by step answer:
It is given that all the steps are 50 m long and have a height of $\dfrac{1}{4}m$ and a tread of $\dfrac{1}{2}m$. We can consider each step as a horizontal layer with increasing width.
Let us consider the 1st step from the top. It has length 50m, height $\dfrac{1}{4}m$ and width $\dfrac{1}{2}m$ .
For the 2nd step, length and height will be the same and the width becomes $\dfrac{1}{2} + \dfrac{1}{2} = \dfrac{2}{2}m$
For the 3rd step, length and height will be the same, and the width increases by $\dfrac{1}{2}m$
For all the steps, the length and height are the same, and the width increases by $\dfrac{1}{2}m$.
We can write the width as an A.P. with $a = \dfrac{1}{2}$ and common difference $d = \dfrac{1}{2}$
Now we can find the sum of the width of the stairs.
Then the sum of the AP is given by the equation,
${S_n} = \dfrac{n}{2}\left( {2a + \left( {n - 1} \right)d} \right)$.
Here we have 15 steps. Then by substituting the values, we get,
$\Rightarrow {S_{15}} = \dfrac{{15}}{2}\left( {2\dfrac{1}{2} + \left( {15 - 1} \right)\dfrac{1}{2}} \right)$
On simplification, we get,
$\Rightarrow {S_{15}} = \dfrac{{15}}{2}\left( {1 + 7} \right)$
On solving the bracket we get,
$\Rightarrow {S_{15}} = \dfrac{{15}}{2} \times 8$
On further simplification we get,
$\Rightarrow {S_{15}} = 60$
Therefore sum of the width is 60m
We can write the sum of the volumes of the steps as a series,
$\Rightarrow V = {V_1} + {V_2} + {V_3} + ... + {V_{15}}$
We know that volume of a step is given by $l \times h \times w$
$\Rightarrow V = {l_1}{h_1}{w_1} + {l_2}{h_2}{w_2} + ... + {l_{15}}{h_{15}}{w_{15}}$
As the length and height of all the steps are equal, we can take them as factors from all the terms.
$\Rightarrow V = l \times h\left( {{w_1} + {w_2} + ... + {w_{15}}} \right)$
Earlier we found that the sum of the width is 60m. on substituting the values, we get,
$\Rightarrow V = 50 \times \dfrac{1}{4} \times 60$
On simplification, we get,
$\Rightarrow V = 750{m^3}$
Therefore, the volume of concrete required to build the terrace is $750{m^3}$.

Note: Alternate approach to solve this problem is given by,
We can consider each step as vertical layers with increasing height.
Volume of the 1st step ${V_1} = 50 \times \dfrac{1}{2} \times \dfrac{1}{4} = \dfrac{{25}}{4}$
${V_2} = 50 \times \dfrac{1}{2} \times \dfrac{2}{4} = \dfrac{{50}}{4}$
${V_3} = 50 \times \dfrac{1}{2} \times \dfrac{3}{4} = \dfrac{{75}}{4}$
This forms an AP with $a = \dfrac{{25}}{4}$ and common difference $d = \dfrac{{25}}{4}$ .
We know that the sum of the AP is given by the equation, ${S_n} = \dfrac{n}{2}\left( {2a + \left( {n - 1} \right)d} \right)$
The total volume is the sum of the series until the 15th term.
$\Rightarrow V = {V_1} + {V_2} + {V_3} + ... + {V_{15}}$
On substituting the values in formula of sum of the AP, we get,
$\Rightarrow V = \dfrac{{15}}{2}\left( {2 \times \dfrac{{25}}{4} + \left( {15 - 1} \right) \times \dfrac{{25}}{4}} \right)$
On simplification we get,
$\Rightarrow V = \dfrac{{15}}{2}\left( {16 \times \dfrac{{25}}{4}} \right)$
$\Rightarrow V = \dfrac{{15}}{2} \times 100$
$\Rightarrow V = 750{m^3}$
Therefore, the volume of concrete required to build the terrace is $750{m^3}$.