Question

A small sphere of mass m is attached to a spring of spring factor k and normal length l. If the sphere rotates with radius r, at frequency v then tension in the spring is

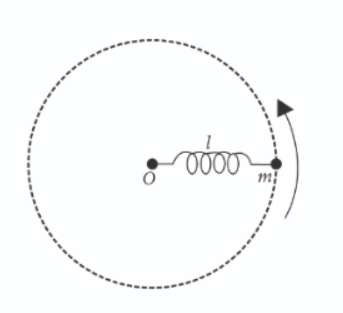
(A) ${{k}^{2}}l$
(B) ${{k}^{2}}(r-l)$
(C) $mr{{(2\pi v)}^{2}}$
(D) $kl$

Answer 1

Here, the spring is unstretched and is in its normal length, so there will be no place for spring force to come into play. Since the body is in circular motion there will act on its centripetal force and because the circular motion is preserved there will be some other force which is balancing the centripetal force.

Complete step by step answer:
Tension will come into the string and this tension will balance the centripetal force
Tension=Centripetal force
$T={{F}_{c}}$
But, ${{F}_{c}}$= $\dfrac{m{{v}^{2}}}{r}$
Where m is the mass of the body, v is the velocity with which it is moving in the circle and r is the radius of the circle. Here, r=l
So, $\dfrac{m{{v}^{2}}}{l}=T$
Also, we can write linear velocity in terms of angular velocity by the relation $v=l\omega$
So, $T=ml{{w}^{2}}$

& \omega =2\pi \nu \\\ & T=ml{{(2\pi \nu )}^{2}} \\\ \end{aligned}$$ Putting l=r we get $$T=mr{{(2\pi \nu )}^{2}}$$ **So, the correct answer is “Option C”.** **Note:** While doing such problems we should be careful to see whether the spring is stretched or not. If spring is unstretched then proceed in an above-shown manner but if there is an extension in the length of the spring then we will have to adjust the restoring spring force into our equations. Also, if there is an extension in the length of the spring then there we will have to take into account the resonance on account of oscillation of the spring.