Question
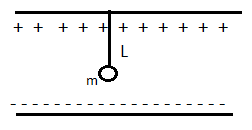
Question: A small sphere carrying a charge \('q'\) is hanging in between two parallel plates by a string of le...
A small sphere carrying a charge ′q′ is hanging in between two parallel plates by a string of length l. The time period of the pendulum is To. When parallel plates are charged, the time period changes to 10T . The ratio of T2T1 is equal to ________
Solution
Find the effective acceleration due to gravity acting on the sphere due to the charged plates and then find the resultant time period to find the required ratio.
Complete step by step answer:
Given data is as follow
A small sphere carrying a charge ′q′ is hanging in between two parallel plates by a string of length l. The time period of the pendulum is To When parallel plates are charged, the time period changes to 10T
We know that the time period of the sphere before charging the plates is
To=2πgl
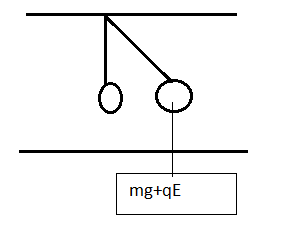
Let the mass of the sphere be
As shown in the above figure a sphere is having an additional weight that is qe along with its own weight
Therefore the effective weight is as follows
mg′=mg+qe
g′=g+mqe
Now this g effects or the final time period, the time period changes as follow
T=2πg′l
⇒T=2πg+mqel
Therefore the ratio of the time period before and after charging the plates is
T2T1=10TTo=2πg+mqel2πgl
⇒TTo=10gg+mqe
Therefore the required ratio of the time periods is
T2T1=10gg+mqe
Note:
Due to the effect of the charge on the plates the weight of the sphere gets changed so the effective gravitational force changes which affects the time period of the pendulum.
