Question
Question: A small particle slides from height H = 45 cm as shown and then loops inside the vertical loop of ra...
A small particle slides from height H = 45 cm as shown and then loops inside the vertical loop of radius R from where a section of angle θ = 60° has been removed. Find R (in cm) such that after losing contact at A and flying through the air, the particle will reach at the point B. Neglect friction everywhere.
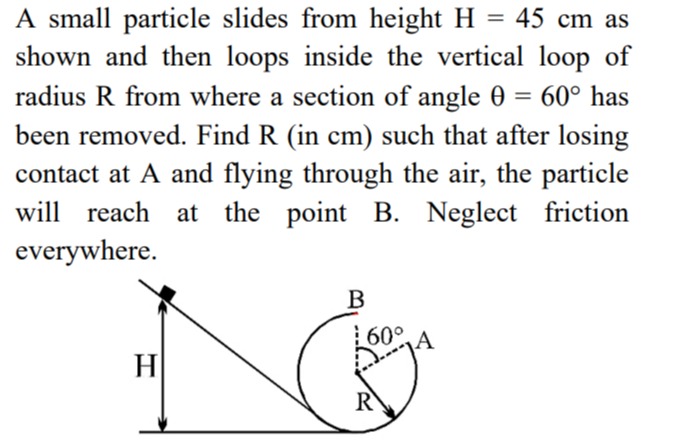
15 cm
15 cm
Solution
The particle falls from rest through a vertical distance H so that at the end of the ramp its speed is v₀ = √(2gH). By energy conservation the speed v₍A₎ at the point A is ½mv₍A₎² = mg(H – y₍A₎) with y₍A₎ the vertical level of A. At A the particle “flies off” with speed v₍A₎ in the direction tangent to the circle. The tangent at A makes an angle of 60° (with the horizontal) so that its horizontal and vertical components are v₍A₎ cos60 and v₍A₎ sin60 respectively. Requiring that the projectile motion bring the particle exactly to the re–entry point B gives two kinematical relations which require that 2g (H – y₍A₎) = g²t² and also that the horizontal displacement equals the chord length (which is R). These conditions combine to require H = 3R so that with H = 45 cm one must have R = 45/3 = 15 cm.
