Question

A small object of uniform density rolls up a curved surface with an initial velocity (v). It reaches up to a maximum height of $\dfrac{3{{v}^{2}}}{4g}$ with respect to the initial position. The object is?

A. Ring
B. Solid Sphere
C. Hollow Sphere
D. Disc

Answer 1

Hint: We will use the conservation of energy formula, which in this case is the sum kinetic energy and the rotational energy is equal to the potential energy, that is: $\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}=mgh$. Since, a rolling action is observed by the object hence, $\omega =\dfrac{v}{r}$. We must also remember that the moment of inertia of a disc is: $I=\dfrac{1}{2}m{{r}^{2}}$.

Complete step-by-step answer:
Let’s remake the diagram by putting in few necessary values in.

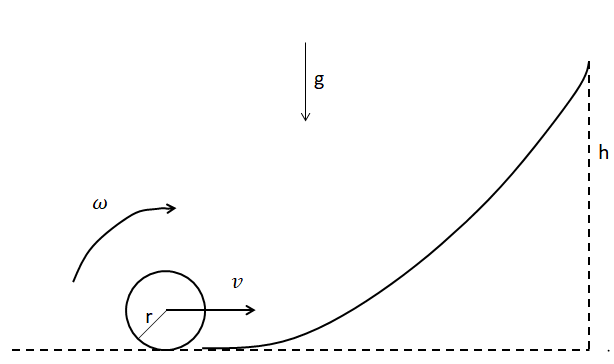
From the options, we can confirm that the body is of a circular nature. We will consider the radius of the object to be (r). We will further consider; the maximum height of the curved path to be (h). The object is rolling up the path with an angular velocity$(\omega )$. As given in the question, the tangential velocity of the object is (v).
Due to the pure rolling action of the object, the object will execute both translational and rotational motion. The sum of the translational and rotational energy will be equal to the potential energy upon reaching the maximum height, due to the conservation of energy. This becomes, $\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}=mgh$. The angular velocity of the object can be given by $\omega =\dfrac{v}{r}$, since the object is rolling up the curved plane and executing pure rolling motion.
Therefore, the conservation of energy formula becomes: $\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{(\dfrac{v}{r})}^{2}}=mgh$.
We will also be substituting in the value of the maximum height (h) as: $h=\dfrac{3{{v}^{2}}}{4g}$.
Hence, the conservation of energy value becomes: $\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{(\dfrac{v}{r})}^{2}}=mg(\dfrac{3{{v}^{2}}}{4g})\Rightarrow \dfrac{1}{2}(\dfrac{I{{v}^{2}}}{{{r}^{2}}})=\dfrac{3}{4}m{{v}^{2}}-\dfrac{1}{2}m{{v}^{2}}\Rightarrow \dfrac{1}{2}(\dfrac{I{{v}^{2}}}{{{r}^{2}}})=\dfrac{1}{4}m{{v}^{2}}$.
Therefore, the value of the moment of Inertia becomes: $(\dfrac{I{{v}^{2}}}{{{r}^{2}}})=\dfrac{1}{2}m{{v}^{2}}\Rightarrow I=\dfrac{1}{2}m{{r}^{2}}$.
This value of the moment of inertia: $I=\dfrac{1}{2}m{{r}^{2}}$, is that of disc.

Note: An alternate method of solving this problem is by taking a standard value of tangential velocity for an object rolling along an incline or a curve. Hence, the standard value of the tangential velocity is: $v=\sqrt{\dfrac{2gh}{1+\dfrac{{{k}^{2}}}{{{r}^{2}}}}}$. We will substitute in the value of (h) as: $h=\dfrac{3{{v}^{2}}}{4g}$in the equation.
Therefore, $v=\sqrt{\dfrac{2gh}{1+\dfrac{{{k}^{2}}}{{{r}^{2}}}}}\Rightarrow {{v}^{2}}=\dfrac{2g}{1+\dfrac{{{k}^{2}}}{{{r}^{2}}}}(\dfrac{3{{v}^{2}}}{4g})\Rightarrow 4g=\dfrac{6g}{1+\dfrac{{{k}^{2}}}{{{r}^{2}}}}\Rightarrow 1+\dfrac{{{k}^{2}}}{{{r}^{2}}}=\dfrac{3}{2}$. Hence, the value of the ratio of the squared value of the radius of gyration to the radius is $\dfrac{{{k}^{2}}}{{{r}^{2}}}=\dfrac{1}{2}\quad \therefore {{k}^{2}}=\dfrac{1}{2}{{r}^{2}}$.
This value of the radius of gyration (k) is for that of a disc.