Question

A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in a X-Y plane with centre at O and constant angular speed $\omega$. If the angular momentum of the system calculated about O and P are denoted by ${{\overrightarrow{L}}_{0}}\text{ and }\overrightarrow{{{L}_{p}}},$ respectively, then:

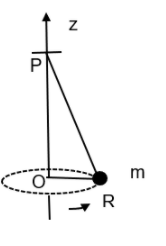
A.${{\overrightarrow{L}}_{0}}\text{ and }\overrightarrow{{{L}_{p}}}$ do not vary with time.
B.${{\overrightarrow{L}}_{0}}\text{ }$varies with time while $\overrightarrow{{{L}_{p}}}$ remains constant
C.${{\overrightarrow{L}}_{0}}$remains constant and $\overrightarrow{{{L}_{p}}}$varies with time.
D.${{\overrightarrow{L}}_{0}}\text{ and }\overrightarrow{{{L}_{p}}}$both vary with time.

Answer 1

The angular momentum is a vector quantity which varies with the point under consideration. Here, the angular momentum of the same body as observed from two different points the centre of rotation O and the fixed-point P are considered.
Formula Used: The angular momentum is calculated using the formula:

& \overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p} \\\ & \text{or} \\\ & \overrightarrow{L}=m(\overrightarrow{r}\times \overrightarrow{v}) \\\ \end{aligned}$$ Where, $$\overrightarrow{L}$$ is the angular momentum $$\overrightarrow{r}$$ is the radius of the circle in which the mass undergoes circular motion $$\overrightarrow{p}$$ is the linear momentum $$v$$ is the linear velocity **Complete answer:** Angular momentum is the measure of linear momentum in a circular motion. It is a vector quantity like the linear momentum. Let us consider the given situation. An object of mass m attached to a fixed string at point P is rotating around a fixed-point O with a constant angular velocity $$\omega $$. We have to determine the angular momenta experienced by the body with respect to point O and P.  We can begin with the point O, the center of rotation. $$\overrightarrow{{{L}_{0}}}=\overrightarrow{r}\times \overrightarrow{p}$$ The linear momentum ‘mv’ being substituted gives, $$\overrightarrow{{{L}_{o}}}=m(\overrightarrow{r}\times \overrightarrow{v})$$ We know that the angular velocity is a constant. Also, the radius of the rotation is a constant. $$\begin{aligned} & \Rightarrow \overrightarrow{{{L}_{o}}}=m(\overrightarrow{OR}\times \overrightarrow{v)} \\\ & \Rightarrow \left| \overline{{{L}_{o}}} \right|=mrv \\\ & \\\ \end{aligned}$$ The magnitude of the angular momentum at O remains constant throughout.  And, the direction of the angular momentum at O is always along the Z-direction. Now, let us consider the angular momentum at point P due to the mass. $$\begin{aligned} & \Rightarrow \overrightarrow{{{L}_{p}}}=m(\overrightarrow{PR}\times \overrightarrow{v}) \\\ & \Rightarrow \overrightarrow{{{L}_{p}}}=m((\overrightarrow{PO}+\overrightarrow{OR})\times \overrightarrow{v}) \\\ \end{aligned}$$ It is clear from the above equation that $$\overrightarrow{PR}$$changes its direction at every instant. As a result, the direction of the angular momentum at P keeps on varying with time. And the magnitude is given by, $$\begin{aligned} & \overrightarrow{{{L}_{p}}}=m\left| \overrightarrow{PR} \right|\overrightarrow{v}\widehat{k} \\\ & \left| \overrightarrow{{{L}_{p}}} \right|=m\left| \overrightarrow{PR} \right|\overrightarrow{v} \\\ \end{aligned}$$ Which remains constant with time. From the above, we can conclude that $$\overrightarrow{{{L}_{o}}}$$remains constant both in direction and magnitude, whereas, $$\overrightarrow{{{L}_{p}}}$$has a constant magnitude, but the direction changes. Therefore, $$\overrightarrow{{{L}_{o}}}$$ remains constant and $$\overrightarrow{{{L}_{p}}}$$varies with time. **The right answer is given by option C.** **Additional Information:** We can calculate the angular momentum by using the angular velocity, $$\overrightarrow{\left| L \right|}=m{{\omega }^{2}}r$$. **Note:** The angular momentum in a closed system remains constant. It is a conserved quantity. As the linear momentum is conserved as long as no external force is applied, the angular momentum is conserved as long as the torque is zero.