Question

A small mass $m$, attached to one end of a spring with a negligible mass and an unstretched length $L$, executes vertical oscillations with angular velocity ${\omega _0}$. When the mass is rotated with an angular speed $\omega$ by holding the other end of the spring at a fixed point, the mass moves uniformly in a circular path in a horizontal plane. Then the increase in length of the spring during the rotation is:

A. $\dfrac{{{\omega ^2}L}}{{\omega _0^2 - {\omega ^2}}}$
B. $\dfrac{{\omega _0^2L}}{{{\omega ^2} - \omega _0^2}}$
C. $\dfrac{{{\omega ^2}L}}{{\omega _0^2}}$
D. $\dfrac{{\omega _0^2L}}{{{\omega ^2}}}$

Answer 1

Use the expression for Newton’s second law of motion. Use the expression for the centripetal force and spring force acting on the spring. Also use the formula for the angular speed in terms of spring constant and mass of the spring. Draw a free body diagram of the mass suspended to the spring and apply Newton’s second law of motion to it in the horizontal direction.

Formulae used:
The Expression for Newton’s second law is
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is net force acting on the object, $m$ is mass of the object and $a$ is acceleration of the object.
The restoring force ${F_S}$ in the spring is
${F_S} = kx$ …… (2)
Here, $k$ is the spring constant of the spring and $x$ is the displacement of the spring.
The centripetal force ${F_C}$ acting on an object is
${F_C} = mR{\omega ^2}$ …… (3)
Here, $m$ is the mass of the object, $R$ is radius of the circular path and $\omega$ is angular speed of the object.
The angular velocity $\omega$ is given by
$\omega = \sqrt {\dfrac{k}{m}}$ …… (4)
Here, $k$ is the spring constant and $m$ is the mass of the spring.

Complete step by step answer:
We have given that the mass $m$ is attached to one end of the spring and the unstretched length of the spring is $L$. The initial angular velocity of this system is ${\omega _0}$ and the angular velocity of the mass when it is rotated in the horizontal circle is $\omega$.We are asked to calculate the increase in length of the spring during the rotation.

Let $x$ be the increase in length of the spring. Rewrite equation (4) for the initial angular velocity.
${\omega _0} = \sqrt {\dfrac{k}{m}}$
$\Rightarrow k = m\omega _0^2$
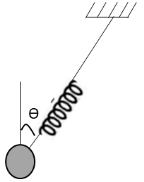
Let us first draw a free body diagram of the mass and spring when it is performing horizontal circular motion.

Let us apply Newton’s second law of motion to the mass in the horizontal direction.
$F = kx\sin \theta$
Here, $k$ is spring constant and $F$ is the centrifugal force on the mass in circular motion.
Substitute $mR{\omega ^2}$ for $F$ in the above equation.
$mR{\omega ^2} = kx\sin \theta$
From the free body diagram, substitute $\left( {L + x} \right)\sin \theta$ for $R$ and $m\omega _0^2$ for $k$ in the above equation.
$m\left( {\left( {L + x} \right)\sin \theta } \right){\omega ^2} = \left( {m\omega _0^2} \right)x\sin \theta$
$\Rightarrow \left( {L + x} \right){\omega ^2} = \omega _0^2x$
$\Rightarrow {\omega ^2}L + {\omega ^2}x = \omega _0^2x$
$\Rightarrow \omega _0^2x - {\omega ^2}x = {\omega ^2}L$
$\Rightarrow \left( {\omega _0^2 - {\omega ^2}} \right)x = {\omega ^2}L$
$\therefore x = \dfrac{{{\omega ^2}L}}{{\omega _0^2 - {\omega ^2}}}$
Therefore, the increase in length of the spring is $\dfrac{{{\omega ^2}L}}{{\omega _0^2 - {\omega ^2}}}$.

Hence, the correct option is A.

Note: The students should not get confused that why we have substituted the formula for centripetal force at the place of centrifugal force in the solution. But the students should keep in mind that the centrifugal force has the same magnitude as that of the centripetal force but direction is opposite to that of the centripetal force. So, we can use the formula for centripetal force for centrifugal force.