Question
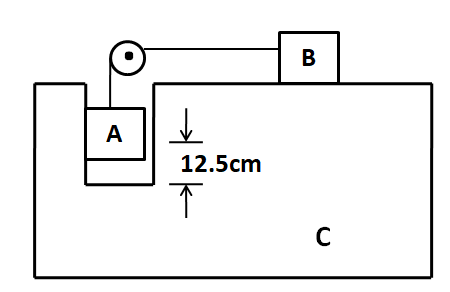
Question: A small, light pulley is attached with a block C of mass \(4kg\) as shown in the figure. Block B of ...
A small, light pulley is attached with a block C of mass 4kg as shown in the figure. Block B of mass 1.5kg is placed on the top horizontal surface of C. Another block A of mass 2kg is hanging from a string, attached with B and passing over the pulley. Taking g=10ms−2 and neglecting friction, calculate the acceleration of each block when the system is released from rest.
Solution
To solve this question, we need to consider the accelerations of blocks A and B with respect to block C. Then we have to apply Newton’s second law of motion for all three blocks. On solving the equations thus obtained, we will get the required accelerations of the blocks.
Complete step by step answer:
Since there is no net external force on the system of the three blocks A, B, and C, so from Newton’s second law of motion we can say that the acceleration of the center of mass of this system should be equal to zero.
Now, we can observe that block A has a tendency to accelerate downwards, the block B has a tendency to accelerate towards the left. So block C will have to move rightwards so as to keep the centre of mass at rest.
Let the acceleration of the block C with respect to the ground be a rightwards.
Also, let the acceleration of block B and C with respect to the block C be aB and aC respectively. So the acceleration of the block B with respect to the ground becomes (aB−a).
Considering the FBD of block B we have
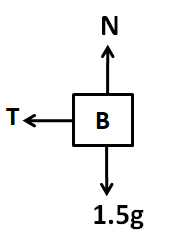
Applying Newton’s second law in the horizontal direction, we have
T=1.5(aB−a) ……………….(1)
Since block C is moving towards the right, and block A is moving downwards, there must be some horizontal force on block A towards the right which will make it move with the same acceleration of a rightwards. Let it be H. So now we consider the FBD of block A as below.
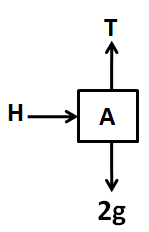
Applying Newton’s second law in the horizontal direction, we have
H=2a ……………..(2)
Since the string connecting A and B is inextensible, so the leftward acceleration of the block B with respect to C must be equal to the downward acceleration of A.
So the downward acceleration of A is equal to aB.
Now, applying second law in the vertical direction, we get
2g−T=2aB ………………...(3)
Finally we consider the FBD of block C as below.
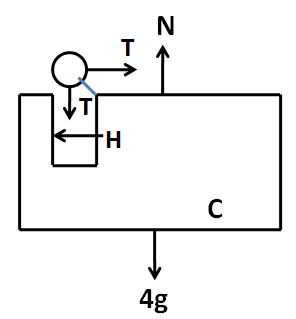
Applying Newton’s second law in the horizontal direction, we have
T−H=4a …………..(4)
Putting (2) in (4) we get
T−2a=4a
⇒T=6a …………………..(5)
Putting this in (1) we get
6a=1.5(aB−a)
⇒7.5a=1.5aB
Dividing by 1.5 both the sides, we get
aB=5a …………………...(6)
Putting (5) and (6) in (3) we get
2g−6a=10a
⇒16a=2g
Dividing both sides by 16 we get
a=8g
⇒a=810=1.25ms−2 …………………...(7)
Putting this in (6) we get
aB=5×1.25
⇒aB=6.25ms−2 ………………...(8)
Now, the acceleration of block B with respect to ground is (aB−a). So from (7) and (8) it becomes equal to 5ms−2 leftward.
Finally, the acceleration of block A in vertically downward direction is aB=6.25ms−2, and in the rightward direction is a=1.25ms−2. So its acceleration with respect to ground becomes
aCG=6.252+1.252
⇒aB=6.37ms−2
Hence, the accelerations of blocks A, B and C are 1.25ms−2, 5ms−2, and 6.37ms−2 respectively.
Note: It might appear by looking at the figure that there is no force on the block C so it should remain at rest. But there are two internal forces, one is the force of tension and the other is the contact force between A and C which will move it in the horizontal direction.
