Solveeit Logo
Login

Question

Question: A small hole is made in a disc of mass M and radius R at a distance \(\dfrac{R}{4}\) from the centre...

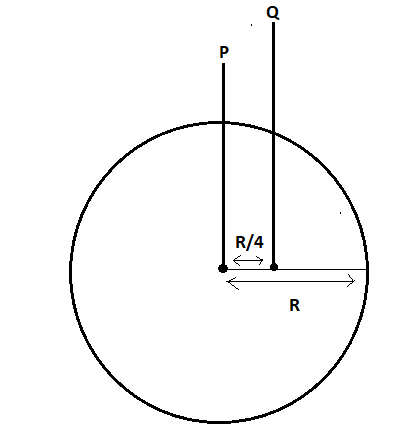
A small hole is made in a disc of mass M and radius R at a distance R4\dfrac{R}{4} from the centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
A. MR29\dfrac{{M{R^2}}}{9}
B. 516MR2\dfrac{5}{{16}}M{R^2}
C. 916MR2\dfrac{9}{{16}}M{R^2}
D. 54MR2\dfrac{5}{4}M{R^2}

Explanation

Solution

Use parallel axis theorem to find the moment of inertia of the disc about horizontal peg.

Complete step by step answer:
We are given that a small hole is made in a disc of mass M and radius R at a distance R4\dfrac{R}{4} from the centre. The disc is supported on a horizontal peg through this hole.
We have to calculate the moment of inertia of the disc around the horizontal peg at point Q.
Moment of inertia is a quantity expressing a body's tendency to resist angular acceleration, which is the sum of the products of the mass of each particle in the body with the square of its distance from the axis of rotation.
Parallel axis theorem states that the moment of inertia of a body about an axis parallel to the body passing through its center is equal to the sum of moment of inertia of body about the axis passing through the center and product of mass of the body times the square of distance between the two axes.
Points P and Q are parallel.
Moment of inertia at point Q is equal to the moment of inertia at point P plus product of mass of the body times the square of distance from the centre.
IQ=IP+M(R4)2 IP=MR22 ⇒IQ=MR22+M(R4)2 ⇒IQ=MR22+MR216 ⇒IQ=8MR2+MR216 ⇒IQ=916MR2  {I_Q} = {I_P} + M{\left( {\dfrac{R}{4}} \right)^2} \\\ {I_P} = \dfrac{{M{R^2}}}{2} \\\ \Rightarrow {I_Q} = \dfrac{{M{R^2}}}{2} + M{\left( {\dfrac{R}{4}} \right)^2} \\\ \Rightarrow {I_Q} = \dfrac{{M{R^2}}}{2} + \dfrac{{M{R^2}}}{{16}} \\\ \Rightarrow {I_Q} = \dfrac{{8M{R^2} + M{R^2}}}{{16}} \\\ \Rightarrow {I_Q} = \dfrac{9}{{16}}M{R^2} \\\
The correct answer is Option C, which is 916MR2\dfrac{9}{{16}}M{R^2}

Note: Moment of Inertia of a body is also defined as the ratio of the net angular momentum of a system to its angular velocity around a principal axis.
I=LwI = \dfrac{L}{w}, L is the angular momentum and w is the angular velocity.