Question

A small freely oriented electric dipole of moment $P$ is placed at the centre of a charged hemispherical cup of surface charge density $\sigma {\text{ C/}}{{\text{m}}^{\text{2}}}$ with dipole moment vector along axis of cup as shown. Find the period of small oscillations of the dipole about the diametrical axis of the base of the cup. The moment of inertia of dipole about the given axis is $I$.

Answer 1

In this question, the concept of the electric field will be used. Finding the electric field intensity due to the dipole, will help us get the time period of the small oscillations of the dipole.

Complete step by step answer:
First of all, we have to find the electric field intensity of the charged hemispherical shell, because of which there is an effect on the dipole, and it is oscillating.
First of all, we should know what a dipole is; a dipole is a combination of two opposite charges ( $q$ and $-q$ ) that are separated by a distance $2a$.
Now let us consider a very tiny circular strip (ring) on the hemisphere at a vertical distance $x$, radial distance $r$ and at an angle $\theta$, as shown in the diagram. $R$, being the radius of the charged hemisphere.

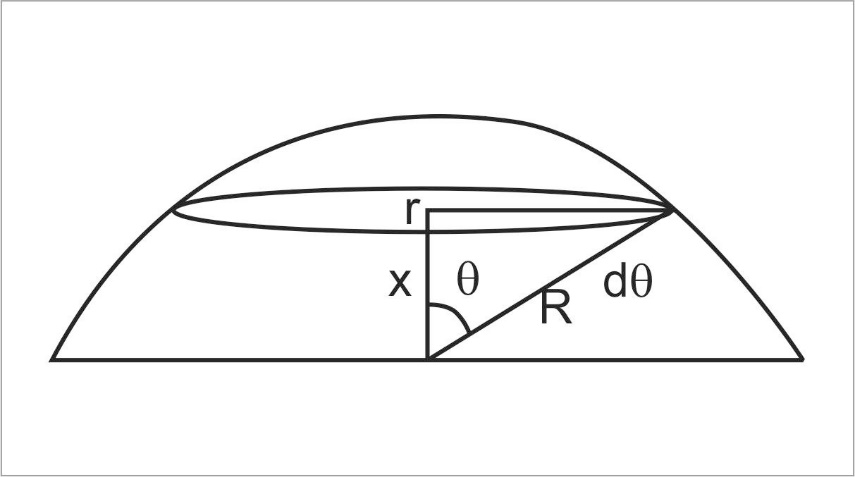
As we know that the electrical Field due to the single ring is,
${E_{ring}} = \dfrac{{KQx}}{{{{\left( {{\text{distance}}} \right)}^3}}}$
Now we substitute the values to obtain,
$\Rightarrow {E_{ring}} = \dfrac{{KQR\cos \theta }}{{{{\left( {{x^2} + {r^2}} \right)}^{\dfrac{3}{2}}}}}..............\left( {\because x = R\cos \theta } \right)$
Now, we simplify the above expression as,
$\Rightarrow {E_{ring}} = \dfrac{{KQR\cos \theta }}{{{{\left( {{R^2}{{\cos }^2}\theta + {R^2}{{\sin }^2}\theta } \right)}^{\dfrac{3}{2}}}}}$
After simplification, we get
$\Rightarrow {E_{ring}} = \dfrac{{KQR\cos \theta }}{{{{\left( {{R^2}} \right)}^{\dfrac{3}{2}}}}}.....................\left( {\because {{\sin }^2}\theta + {{\cos }^2}\theta = 1} \right)$
$\Rightarrow {E_{ring}} = \dfrac{{KQ\cos \theta }}{{{R^2}}}......\left( 1 \right)$
As we know that, $Q = \sigma \times Area$
$\Rightarrow Q = \sigma \times 2\pi rRd\theta$
After simplification we get
$\Rightarrow Q = \sigma \times 2\pi \left( {R\sin \theta } \right)Rd\theta$
$\Rightarrow Q = 2\pi \sigma {R^2}\sin \theta d\theta$
Now substituting the expression for $Q$ in equation (1) as,
$\Rightarrow {E_{ring}} = \dfrac{{2\pi {R^2}\sin \theta \sigma K\cos \theta }}{{{R^2}}}d\theta$
$\Rightarrow {E_{ring}} = 2\pi \sigma K\sin \theta \cos \theta d\theta$
Now, total electric field will be,
$E = \int\limits_{\theta = 0}^{\theta = \dfrac{\pi }{2}} {2\pi K\sigma \sin \theta \cos \theta d\theta }$
$\Rightarrow E = \pi K\sigma \int\limits_{\theta = 0}^{\theta = \dfrac{\pi }{2}} {\sin 2\theta d\theta }$
After integration we get,
$\Rightarrow E = \pi K\sigma ...............\left( {\because \int\limits_{\theta = 0}^{\theta = \dfrac{\pi }{2}} {\sin 2\theta d\theta } = 1} \right)$
$\Rightarrow E = \dfrac{\sigma }{{4{\varepsilon _0}}}...................\left( {\because K = \dfrac{1}{{4\pi {\varepsilon _0}}}} \right)$
Therefore, the total electric field intensity due to the hemisphere is $E = \dfrac{\sigma }{{4{\varepsilon _o}}}$
Now the time period of oscillation of a dipole is given as $2\pi \sqrt {\dfrac{I}{{PE}}}$
Where $P$ is the moment of the dipole, $E$ is the electric field generated from the surroundings and $I$ is the moment of inertia about the given axis.
Putting the values we get the time period as,
$T = 2\pi \sqrt {\dfrac{I}{{PE}}}$
Now, substitute the expression of the electric field as,
$\Rightarrow T = 2\pi \sqrt {\dfrac{I}{{P\dfrac{\sigma }{{4{\varepsilon _0}}}}}}$
After simplification we get,
$\therefore T = 4\pi \sqrt {\dfrac{{I{\varepsilon _0}}}{{P\sigma }}}$
Thus, the period of small oscillations of dipole about diametrical axis of base of cup is $T = 4\pi \sqrt {\dfrac{{I{\varepsilon _0}}}{{P\sigma }}}$.

Note: The time period depends on the Electric Field Intensity, the moment of inertia and the moment of the dipole. Hence any changes in these will change the time period of the oscillation.