Question

A small electric dipole is placed at origin with its axis being directed along the positive x-axis. The direction of electric field due to the dipole at a point $\left( 1m,\sqrt{2}m,0 \right)$ is along the:
(A). z-axis
(B). y-axis
(C). x-axis
(D). line y=x

Answer 1

Hint: To calculate the direction of electric field due to dipole we have to break the dipole into components along and perpendicular to the line joining that point and the dipole. And then add the electric field due to both the components.

Complete Step By Step answer:
Dipole is the name given to the system in which two equal and oppositely charged particles are kept very close to each other. The direction of dipole is from negative charge to positive charge. The electric field of dipole at its axis is given by the formula$\dfrac{2kp}{{{r}^{3}}}$ … (1), where p is dipole strength of the dipole and r is distance of the point (where electric field is to be found) from dipole. The electric field of dipole at its perpendicular bisector is $\dfrac{kp}{{{r}^{3}}}$… (2). Electric field at any point due to dipole can be found by taking one component of dipole along the line joining that point and the dipole and other component of dipole perpendicular to the line joining that point and the dipole.
Now to find the electric field at $\left( 1m,\sqrt{2}m,0 \right)$, we will join the dipole to this point by a vector. That vector will be
$1\overset{\wedge }{\mathop{i}}\,+\sqrt{2}\overset{\wedge }{\mathop{j}}\,$ , the angle it makes with x-axis is $\theta ={{\tan }^{-1}}\sqrt{2}$ . The component of dipole along the line will be $p\cos \theta$ , let us call it ${{p}_{1}}$ . Electric field due to this dipole (using formula 1) is $\dfrac{2kp\cos \theta }{{{r}^{3}}}$ . Its direction will be along the vector. So, in vector form electric field can be written as
${{E}_{{{p}_{1}}}}=\dfrac{2kp\cos \theta }{{{r}^{3}}}\times \cos \theta \overset{\wedge }{\mathop{i}}\,+\dfrac{2kp\cos \theta }{{{r}^{3}}}\times \sin \theta \overset{\wedge }{\mathop{j}}\,=\dfrac{2kp}{{{r}^{3}}}\times \dfrac{1}{3}\overset{\wedge }{\mathop{i}}\,+\,\dfrac{2kp}{{{r}^{3}}}\times \dfrac{\sqrt{2}}{3}\overset{\wedge }{\mathop{j}}\,$
The component of dipole perpendicular to the line will be $p\sin \theta$ , let us call it ${{p}_{2}}$ . Electric field due to this dipole (using formula 2) is $\dfrac{kp\sin \theta }{{{r}^{3}}}$ . Its direction will be perpendicular to the vector. So, in vector form electric field can be written as
${{E}_{{{p}_{2}}}}=-\dfrac{kp\sin \theta }{{{r}^{3}}}\times \sin \theta \overset{\wedge }{\mathop{i}}\,+\dfrac{kp\sin \theta }{{{r}^{3}}}\times \cos \theta \overset{\wedge }{\mathop{j}}\,=-\dfrac{kp}{{{r}^{3}}}\times \dfrac{2}{3}\overset{\wedge }{\mathop{i}}\,+\,\dfrac{kp}{{{r}^{3}}}\times \dfrac{\sqrt{2}}{3}\overset{\wedge }{\mathop{j}}\,$

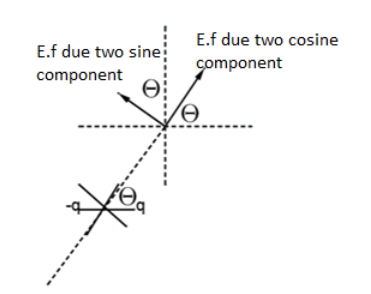
On adding electric field due to both the component we get
$\dfrac{\sqrt{2}kp}{{{r}^{3}}}\overset{\wedge }{\mathop{j}}\,$
So the direction of the net electric field is only along the y-axis.
Hence the correct option is B.

Note: For the direction of electric along the axis of dipole we must remember that, if the point is closer to the positive charge, the direction of electric field is in the direction of dipole, if the point is closer to the negative charge, the direction of electric field is opposite to direction of dipole. The direction of electric field along the perpendicular bisector is opposite to the direction of the dipole.