Solveeit Logo
Login

Question

Question: A small electric dipole is of dipole moment p. The electric potential at a distance ‘r’ from the cen...

A small electric dipole is of dipole moment p. The electric potential at a distance ‘r’ from the center and making an angle θ\theta with the axis of dipole will be:

Explanation

Solution

Electric dipole is a couple of opposite charges given by q and -q. they are separated by the distance d. In this given space the direction of the dipole is always from -q to positive charge q. In the question we need to find potential at distance r from center. It is making an angle θ\theta with the axis.

Formula Used:
V=q4πε0R cos⁡θ=y2+z2−x22yz (1+xn)=1+nx for x<<1  V = \dfrac{q}{{4\pi {\varepsilon _0}R}} \\\ \cos \theta = \dfrac{{{y^2} + {z^2} - {x^2}}}{{2yz}} \\\ (1 + {x^n}) = 1 + nx\,for\,x < < 1 \\\

Complete step-by-step solution:

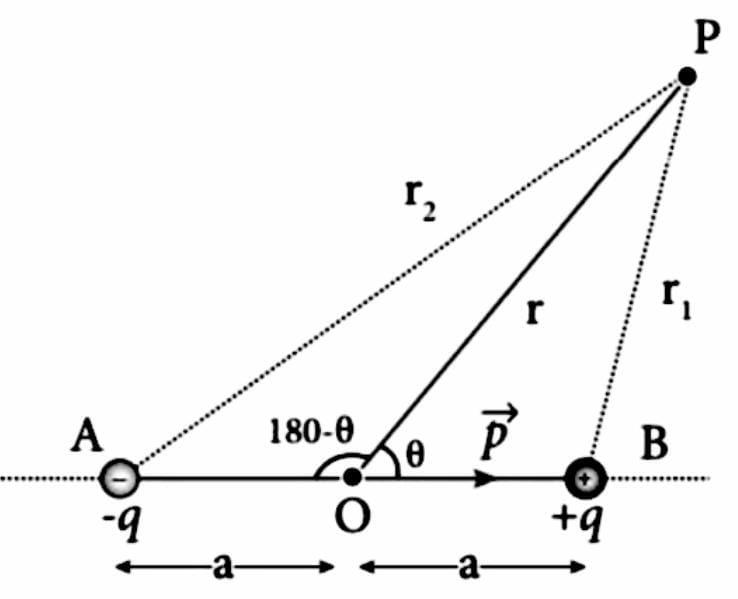
First of all we have the dipole with charges q and -q at the ends.
The potential at the distance ‘r’ can be found out as follows:
First from the figure we will get,

USING, cos⁡θ=y2+z2−x22yz  USING, \\\ \cos \theta = \dfrac{{{y^2} + {z^2} - {x^2}}}{{2yz}} \\\

Cosine formula for any triangle.
Here, z is hypotenuse.
According to our dimensions
cos⁡θ=r2+a2−r122ra ⇒r12=r2+a2−2racos⁡θ  \cos \theta = \dfrac{{{r^2} + {a^2} - {r_1}^2}}{{2ra}} \\\ \Rightarrow {r_1}^2 = {r^2} + {a^2} - 2ra\cos \theta \\\
By taking square root on both sides we get,
r1=(r2+a2−2racos⁡θ)12 taking ′r′ common ⇒r1=r[1−arcos⁡θ]12  {r_1} = {({r^2} + {a^2} - 2ra\cos \theta )^{\dfrac{1}{2}}} \\\ taking\,'r'\,common \\\ \Rightarrow {r_1} = r{\left[ {1 - \dfrac{a}{r}\cos \theta } \right]^{\dfrac{1}{2}}} \\\
Now using the identity,
(1+xn)=1+nx for x<<1(1 + {x^n}) = 1 + nx\,for\,x < < 1
We get,
r1=r[1−arcos⁡θ] this gives ⇒r1=r−acos⁡θ ⇒r2=r+acos⁡θ  {r_1} = r\left[ {1 - \dfrac{a}{r}\cos \theta } \right] \\\ this\,gives \\\ \Rightarrow {r_1} = r - a\cos \theta \\\ \Rightarrow {r_2} = r + a\cos \theta \\\
We know for the potential we need to find individual potentials from each charge and add them. So,
V=q4πε0R adding all ⇒V=q4πε0r1+q4πε0r2   V = \dfrac{q}{{4\pi {\varepsilon _0}R}} \\\ adding\,all \\\ \Rightarrow V = \dfrac{q}{{4\pi {\varepsilon _0}{r_1}}} + \dfrac{q}{{4\pi {\varepsilon _0}{r_2}}} \\\ \\\
Putting the values taken found out above and solving,
⇒q4πε0[1r−acos⁡θ−1r+acos⁡θ] ⇒q4πε0[r+acos⁡θ−r+acos⁡θr2−a2cos⁡2θ]  \Rightarrow \dfrac{q}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{1}{{r - a\cos \theta }} - \dfrac{1}{{r + a\cos \theta }}} \right] \\\ \Rightarrow \dfrac{q}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{r + a\cos \theta - r + a\cos \theta }}{{{r^2} - {a^2}{{\cos }^2}\theta }}} \right] \\\
Further solving the equations and neglecting a as it is very small we get
As p=q(2a) ⇒V=pcos⁡θ4πε0(r2−a2cos⁡2θ) ⇒V=pcos⁡θ4πε0(r2).....(if a is small)  As\,p = q(2a) \\\ \Rightarrow V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _0}({r^2} - {a^2}{{\cos }^2}\theta )}} \\\ \Rightarrow V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _0}({r^2})}}.....(if\,a\,is\,small) \\\

Note: Potential at the point is always an addition of potential due to all charges/dipoles. Potential negative means whatever the system is under study it is stable. If potential is positive it is an unstable system. Force varies inversely with square of the distance and potential inversely with first power of distance.