Question

A small disc of mass m slides down a hill of height without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill (as shown in the figure). Due to friction between the disc and the plank, the disc slows down and beginning with a certain moment, moves in one piece with the plank.

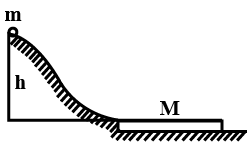
Find the total work performed by the frictional forces in this process. Given reduce mass of the system $\mu = \dfrac{{mM}}{{m + M}}$
A. $\mu gh$
B. $- \mu gh$
C. $2\mu gh$
D. $- 2\mu gh$

Answer 1

When the disc rolls down the hill, its gravitational potential energy changes into kinetic energy. After the collision the change in the kinetic energies is equal to the work done by the frictional forces.

Complete step by step solution:
As the disc is initially at rest at the top of the hill. So its initial kinetic energy is 0. Its gravitational potential energy is given by $mgh$ .
When the disc is sliding down the plank, its gravitational potential energy changes into kinetic energy. If $v$ is the velocity of the disc while sliding down the hill. Then,
$\dfrac{1}{2}m{v^2} = mgh \Rightarrow v = \sqrt {2gh}$ …..(1)

As the disc slows down and begins with a certain moment, moves in one piece with the plank. Their combined mass will be $\left( {m + M} \right)$. If ${v_1}$ is the new velocity of both disc and the plank. Then,
Initial momentum of the disc = momentum of the combined disc and the plank.
$mv = \left( {m + M} \right){v_1}$
$\Rightarrow {v_1} = \dfrac{{mv}}{{\left( {m + M} \right)}}$
Putting the value of $v$ from equation (1), we get
${v_1} = \dfrac{{m\sqrt {2gh} }}{{\left( {m + M} \right)}}$
The kinetic energy ${k_2}$of both the plank and the disc is given by $\dfrac{1}{2}\left( {m + M} \right){v_1}^2$
$\Rightarrow {k_2} = \dfrac{1}{2}\left( {m + M} \right){v_1}^2$
$\Rightarrow {k_2} = \dfrac{1}{2}\left( {m + M} \right)\dfrac{{{m^2}.2gh}}{{{{\left( {m + M} \right)}^2}}}$
$\Rightarrow {k_2} = \dfrac{{{m^2}gh}}{{\left( {m + M} \right)}}$
The total work done by the frictional force during this process is equal to the change in the kinetic energy.

Total work done = $\dfrac{{{m^2}gh}}{{\left( {m + M} \right)}} - mgh$
$= \dfrac{{{m^2}gh - mgh\left( {m + M} \right)}}{{\left( {m + M} \right)}} = \dfrac{{ - mMgh}}{{\left( {m + M} \right)}}$
Given reduce mass of the system $\mu = \dfrac{{mM}}{{m + M}}$
Therefore above equation reduces to $- \mu gh$

Hence the correct option is (B).

Note: When a body at rest is brought into motion and collides with another body. Its initial and final momentum remains the same. The loss in kinetic energy is used to do the work.