Question

A small disc and a thin uniform rod of length $l$, whose mass is $\eta$ times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horizontal direction and perpendicular to the rod, with velocity $v$, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after collision. At what value of $\eta$will the velocity of the disc after the collision be equal to zero? Reverse its direction?

Answer 1

The system is made with a disc moving with velocity $v$ and a rod at rest. The angular as well the translational momentum of the system is conserved. In elastic collision, the kinetic energy is conserved. Using equations from the above laws of conservation, we can calculate the final velocity of the disc, angular velocity of the rod and the value of $\eta$.

Formulas used:
$mv\dfrac{l}{2}+0=mv'\dfrac{l}{2}+\dfrac{\eta m{{l}^{2}}}{12}\omega$
$mv=mv'+\eta m{{v}_{c}}$
$\dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}mv{{'}^{2}}+\dfrac{1}{2}\eta mv_{c}^{2}+\dfrac{1}{2}\dfrac{\eta m{{l}^{2}}}{12}{{\omega }^{2}}$

Complete step-by-step solution:

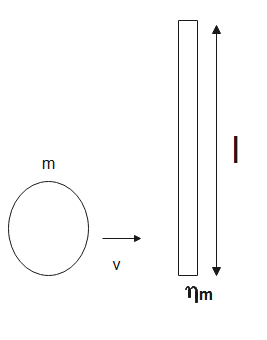
Given the mass of the rod is $\eta$ times more than the mass of the disc. The system of rod and disc is an isolated system as no external forces are acting on it, thus momentum of the system is conserved.

After collision of the disc with the rod, the rod will rotate about its centre of mass. Hence, its axis will be in the centre.

Applying conservation of angular momentum of the system, we get,
$mv\dfrac{l}{2}+0=mv'\dfrac{l}{2}+\dfrac{\eta m{{l}^{2}}}{12}\omega$
Here, $v'$ is the final velocity of the disc
$\omega$ is the angular velocity of the rod

Applying conservation of linear momentum to the system, we get,
$mv=mv'+\eta m{{v}_{c}}$
Here, ${{v}_{c}}$ is the velocity of the centre of mass

Substituting eq (2) in eq (1), we get,
$\begin{aligned} & mv\dfrac{l}{2}+0=mv'\dfrac{l}{2}+\dfrac{\eta m{{l}^{2}}}{12}\omega \\\ & \Rightarrow (mv'+\eta m{{v}_{c}})\dfrac{l}{2}=mv'\dfrac{l}{2}+\dfrac{\eta m{{l}^{2}}}{12}\omega \\\ & \Rightarrow \eta m{{v}_{c}}\dfrac{l}{2}=\dfrac{\eta m{{l}^{2}}}{12}\omega \\\ & \therefore {{v}_{c}}=\dfrac{l\omega }{6} \\\ \end{aligned}$

The disc collides with the rod elastically; hence the kinetic energy of the system is conserved. Therefore,
$\begin{aligned} & \dfrac{1}{2}m{{v}^{2}}=\dfrac{1}{2}mv{{'}^{2}}+\dfrac{1}{2}\eta mv_{c}^{2}+\dfrac{1}{2}\dfrac{\eta m{{l}^{2}}}{12}{{\omega }^{2}} \\\ & \Rightarrow {{v}^{2}}=v{{'}^{2}}+\eta v_{c}^{2}+\eta \dfrac{{{l}^{2}}{{\omega }^{2}}}{12} \\\ & \Rightarrow {{v}^{2}}-v{{'}^{2}}=\eta v_{c}^{2}+\eta \dfrac{{{l}^{2}}{{\omega }^{2}}}{12} \\\ & \Rightarrow (v-v')(v+v')=\eta v_{c}^{2}+\eta \dfrac{{{l}^{2}}{{\omega }^{2}}}{12} \\\ \end{aligned}$
From eq (2), $v-v'=\eta {{v}_{c}}$ - (3)

Substituting in the above equation,
$\begin{aligned} & (v-v')(v+v')=\eta v_{c}^{2}+\eta \dfrac{{{l}^{2}}{{\omega }^{2}}}{12} \\\ & \Rightarrow \eta {{v}_{c}}(v+v')=\eta v_{c}^{2}+\eta \dfrac{{{l}^{2}}{{\omega }^{2}}}{12} \\\ \end{aligned}$
$\begin{aligned} & {{v}_{c}}=\dfrac{l\omega }{6} \\\ & \Rightarrow \omega =\dfrac{6{{v}_{c}}}{l} \\\ \end{aligned}$

Substituting in above equation, we get,
$\begin{aligned} & \eta {{v}_{c}}(v+v')=\eta v_{c}^{2}+\dfrac{{{l}^{2}}{{\omega }^{2}}}{12} \\\ & \Rightarrow \eta {{v}_{c}}(v+v')=\eta v_{c}^{2}+\dfrac{{{l}^{2}}\dfrac{36v_{c}^{2}}{{{l}^{2}}}}{12} \\\ & \Rightarrow \eta {{v}_{c}}(v+v')=4\eta v_{c}^{2} \\\ \end{aligned}$
$\therefore (v+v')={{v}_{c}}$ - (4)

Adding eq (3) and eq (4), we get,
$\begin{aligned} & 2v=(\eta +1){{v}_{c}} \\\ & \Rightarrow {{v}_{c}}=\dfrac{2}{\eta +1}v \\\ \end{aligned}$

Therefore from eq (4), the value of final velocity of the disc will be-
$\begin{aligned} & (v+v')={{v}_{c}} \\\ & \Rightarrow v'={{v}_{c}}-v \\\ & \Rightarrow v'=\dfrac{2}{\eta +1}v-v \\\ & \therefore v'=\dfrac{1-\eta }{1+\eta }v \\\ \end{aligned}$

Therefore, the final velocity of the disc is $\dfrac{1-\eta }{1+\eta }v$
When $v'=0$,
$\begin{aligned} & \dfrac{1-\eta }{1+\eta }v=0 \\\ & \Rightarrow \eta =1 \\\ \end{aligned}$

For the disc to come to rest, the value of $\eta$ should be 1 and for the disc to change its direction the value of final velocity will be negative with respect to initial velocity, therefore, when for any value $\eta >1$, the disc will change its direction.

The angular velocity of rod will be-
$\begin{aligned} & \omega =\dfrac{6{{v}_{c}}}{l} \\\ & \Rightarrow \omega =\dfrac{6}{l}\times \dfrac{2}{1+\eta } \\\ & \therefore \omega =\dfrac{12}{l(1+\eta )} \\\ \end{aligned}$

Therefore, the final velocity of the disc is $\dfrac{1-\eta }{1+\eta }v$, the angular velocity of the rod is $\dfrac{12}{l(1+\eta )}$. The disc will come to rest for $\eta =1$ and it will change direction for $\eta >1$.

Note:
As the rod has uniform density, its centre of mass will lie in the centre. When the collision is elastic, kinetic energy of the system is conserved. The system possesses kinetic energy due to translational motion of the disc and rotational and translational motion of the rod. When a body has both kinetic energy and translational energy, it is in rolling motion.