Question

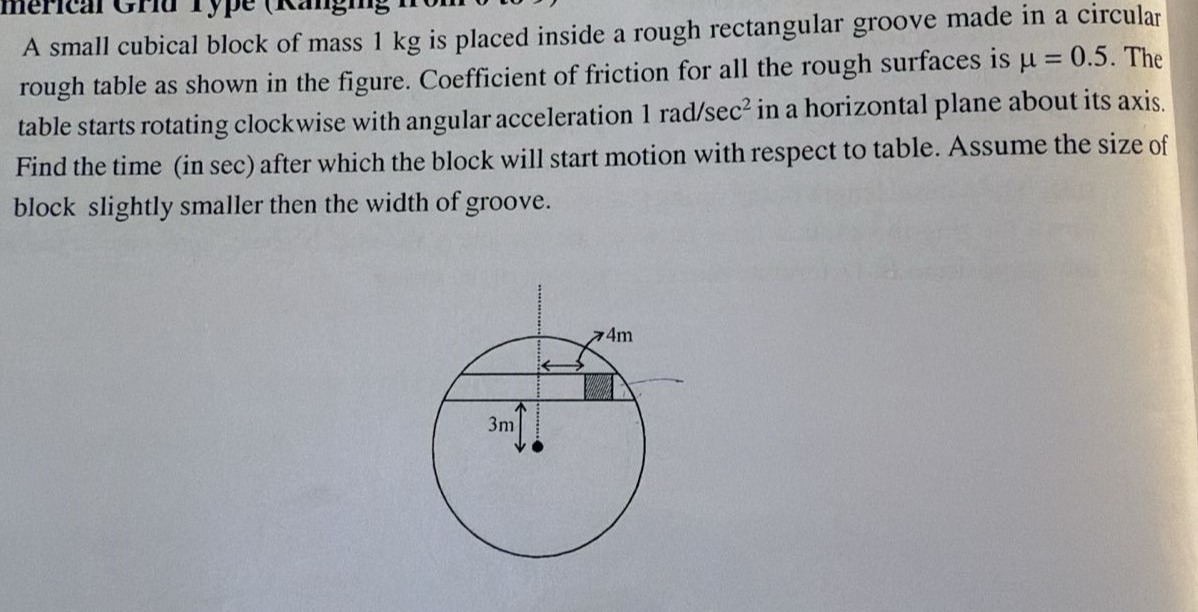
A small cubical block of mass 1 kg is placed inside a rough rectangular groove made in a circular rough table as shown in the figure. Coefficient of friction for all the rough surfaces is $\mu$ = 0.5. The table starts rotating clockwise with angular acceleration 1 rad/sec$^2$ in a horizontal plane about its axis. Find the time (in sec) after which the block will start motion with respect to table. Assume the size of block slightly smaller then the width of groove.

Answer 1

1.41

Answer 2

1. Identify the forces acting on the block in the rotating frame of the table. These include real forces (normal forces and friction) and pseudo forces (centrifugal and Coriolis).

2. Determine the components of these forces along and perpendicular to the groove.

3. When the block is at rest relative to the table, the velocity relative to the rotating frame is zero, so the Coriolis force is zero.

4. The forces perpendicular to the groove are balanced by the normal forces from the walls. The component of the centrifugal force perpendicular to the groove is $m \omega^2 3$. This is balanced by the normal force from the walls, $N_w = m \omega^2 3$.

5. The friction forces opposing motion along the groove are from the bottom ($\mu mg$) and from the walls ($\mu N_w = \mu m \omega^2 3$). The total maximum static friction is $\mu mg + \mu m \omega^2 3$.

6. The force tending to move the block along the groove is the component of the centrifugal force along the groove, which is $m \omega^2 x'$.

7. The block starts moving when the driving force along the groove exceeds the maximum static friction force. At the starting point, $x' = 4$.

8. Set up the inequality $m \omega^2 4 > \mu mg + \mu m \omega^2 3$.

9. Solve the inequality for $\omega^2$: $\omega^2 > \frac{\mu g}{4 - 3 \mu}$.

10. Substitute $\omega = t$ and the given values of $\mu$ and $g$ to find the time t when the motion starts.

The final answer is $\sqrt{2} \approx 1.414$. Rounding to two decimal places gives 1.41.