Question

A small compass needle of magnetic moment $m$ is free to turn about an axis perpendicular to the direction of uniform magnetic field $B$ . The moment of inertia of the needle about the axis is $I$ . The needle is slightly disturbed from its stable position and then released. Prove that it executes simple harmonic motion. Hence deduce the expression for its time period.

Answer 1

We will try to draw a diagram to get a better understanding of the situation. Then we will use the torque produced when a magnet is placed in a magnetic field and compare this with torque during rotational motion. We will deduce the proof for harmonic motion from this. To find the time period, we will find the inertia factor and spring factor form the torque equation in presence of a magnetic field.

Formula used:
$\begin{aligned} & \tau =-M\times B=-MB\sin \theta \\\ & T=2\pi \sqrt{\dfrac{\text{Inertia Factor}}{\text{Spring Factor}}} \\\ \end{aligned}$

Complete step by step answer:
Firstly, we will draw a diagram to understand the situation clearly.

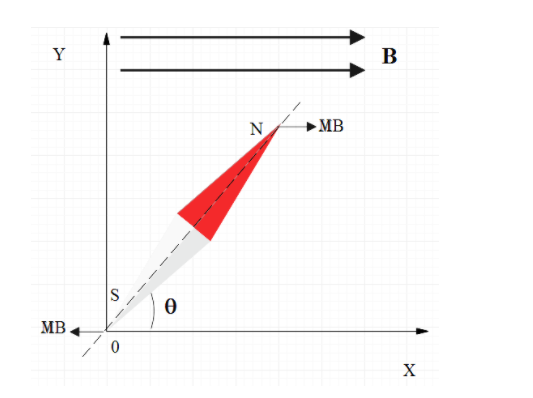
Now, we have the magnetic moment of the compass needle given as $m$ and the magnetic field as $B$ . The needle is slightly disturbed by an angle $\theta$ from its stable position which is $0{}^\circ$ .
Then, the torque experienced by the needle is given by,
$\tau =-M\times B=-MB\sin \theta$
But, $\theta$ is very small. So, $\sin \theta \approx \theta$
$\Rightarrow \tau =-MB\theta$
Now, we will find the torque experienced by the needle due to rotation which is given as,
$\tau =I\alpha$
Here, $I$ is the moment of inertia and $\alpha$ is angular acceleration.
Now, these two torques will be equal.
$\Rightarrow I\alpha =-MB\theta$
We know $\alpha =\dfrac{{{\delta }^{2}}\theta }{\delta {{t}^{2}}}$
$\Rightarrow I\dfrac{{{\delta }^{2}}\theta }{\delta {{t}^{2}}}=-MB\theta$
$\dfrac{{{\delta }^{2}}\theta }{\delta {{t}^{2}}}=-\dfrac{MB}{I}\theta$
This expression is the proof for the motion is simple harmonic.
Now, we will find time period using the equation,
$T=2\pi \sqrt{\dfrac{\text{Inertia Factor}}{\text{Spring Factor}}}$
From the equation $\tau =-MB\theta$ , we can get $\tau \propto \theta$ . We will compare this with the spring equation $F=-kx$ . By comparing these two, we can get the spring constant as,
$k=MB$
The inertia factor will be the moment of inertia of the needle $I$ . Then, the time period will become,
$T=2\pi \sqrt{\dfrac{I}{MB}}$
This is the expression for the time period.

Note:
The important point to be careful while solving this equation is while we are equating the torque due magnetic field to the torque while rotational motion. This is purely based on the law of conservation of energy. The equation of motion of a particle executing simple harmonic motion is given by the expression, $\dfrac{{{\delta }^{2}}x}{\delta {{t}^{2}}}=-\dfrac{k}{m}x$ . Also, we have simply compared the torque equation with the spring equation for obtaining the spring constant.