Question
Question: A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin...
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure). How fast is the light traveling in the liquid?
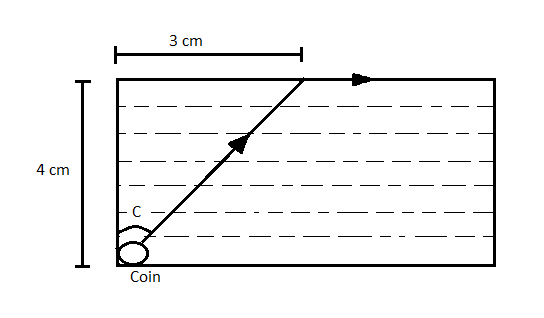
A. 1.2×108 m/s
B. 1.8×108 m/s
C. 2.4×108 m/s
C. 3.0×108 m/s
Solution
Here, the light ray did not emerge out from water (denser medium) to air (rarer medium) We can see from figure that, the angle of refraction is 90∘. Then the incident angle is a critical angle. We can find out the velocity of light in water using the equation which relates the refractive index and sin of critical angle.
Formula used:
sin C =μ1
μ=Velocity of light in liquid(v)Velocity of light in air(c)
R=htanC
sin2a+cos2a=1
sinC=Hypotenuseadjacent side
tanC=CosCsinC
Complete answer:
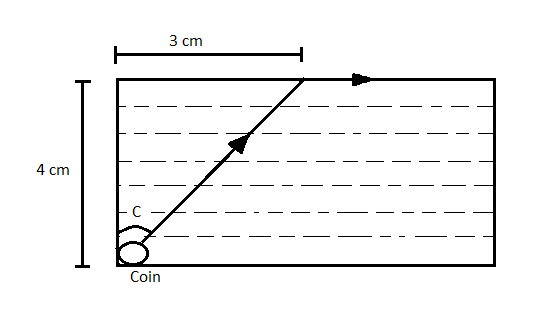
As shown in the figure, the light ray from the coin did not emerge. Therefore, the angle of incidence is the critical angle.
(When the light travels from an optically denser medium to an optically less dense (rarer) medium, angle of incidence where the angle of refraction is 90∘ is known as critical angle.)
From the figure,
sin C=42+323=53
Where, C is the critical angle
We know that,
μ1= sin C
Where, μ is the refractive index.
sin C =μ1
μ=Velocity of light in liquid(v)Velocity of light in air(c)
Therefore,
sinC=cv
We have, c = 3×108m/s
Then,
sinC=3×108v
53=3×108v
v=53×3×108=1.8×108m/s
So, the correct answer is “Option B”.
Note:
This can be solved in another method.
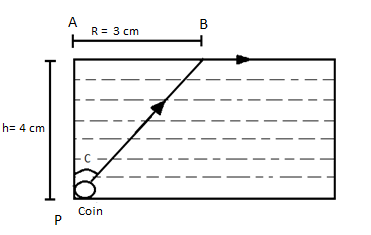
Consider triangle PAB,
We have,
hR=tanC
Where,
R - circle of radius
h- height
R=htanC
R=h×CosCsinC
Since, (sin2a+cos2a=1)
R=h×1−sin2CsinC
We know that,
sin C =μ1
Then,
R=μ2−1h
43=μ2−1h
μ2=925
μ=35=1.67
We know that,
μ=vc
v=1.663×108=1.8×108m/s
