Question

A small charged bead can slide on a circular frictionless, insulating wire frame. A point like dipole is fixed at the centre of circle, dipole moment is $\overrightarrow{p}$. Initially the bead is on the plane of symmetry of the dipole. Bead is released from rest. Ignore the effect of gravity. Mark the correct options

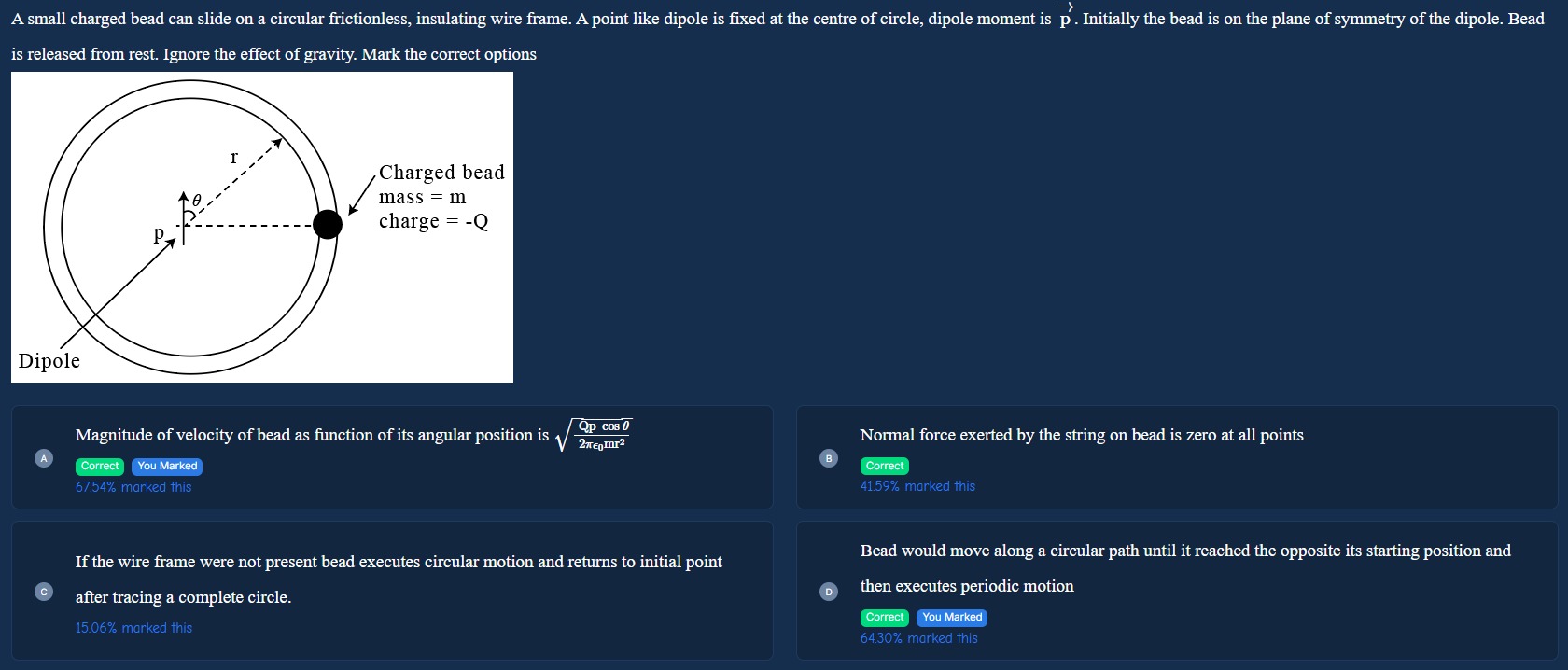
• A. Magnitude of velocity of bead as function of its angular position is $\sqrt{\frac{Qp\cos\theta}{2\pi\epsilon_0mr^2}}$
• B. Normal force exerted by the string on bead is zero at all points
• C. If the wire frame were not present bead executes circular motion and returns to initial point after tracing a complete circle.
• D. Bead would move along a circular path until it reached the opposite its starting position and then executes periodic motion

Answer 1

Answer: (A), (B), (D)

A, B, D

Answer 2

The electric potential due to a dipole $\vec{p}$ at a position $\vec{r}$ is $V(\vec{r}) = \frac{1}{4\pi\epsilon_0} \frac{\vec{p} \cdot \vec{r}}{r^3}$.

Let $r$ be the radius of the circular wire frame. Let $\theta$ be the angle between the dipole moment $\vec{p}$ and the position vector $\vec{r}$ of the bead from the center. The potential at the position of the bead is $V(\theta) = \frac{p \cos\theta}{4\pi\epsilon_0 r^2}$.

The charge of the bead is $-Q$. The potential energy of the bead is $U(\theta) = (-Q) V(\theta) = -\frac{Qp \cos\theta}{4\pi\epsilon_0 r^2}$.

The bead is released from rest at the plane of symmetry, which corresponds to $\theta_0 = \pi/2$. The initial potential energy is $U_0 = U(\pi/2) = 0$.

By conservation of energy, $\frac{1}{2}mv^2 - \frac{Qp \cos\theta}{4\pi\epsilon_0 r^2} = 0$.

Therefore, the magnitude of velocity is $v = \sqrt{\frac{Qp \cos\theta}{2\pi\epsilon_0 mr^2}}$.

The normal force exerted by the wire frame on the bead is zero at all points.

The bead moves along a circular path until it reaches the opposite its starting position and then executes periodic motion.