Question

A small charged ball having mass $m$ and charge $q$ is suspended from a rigid support by means of an inextensible thread of length $l$. It is made to rotate on a horizontal circular path in a uniform, time independent magnetic field of induction $B$ which is directed upward. The time period of revolution of the ball is ${{T}_{0}}$. If the radius of the circular path on which the ball moves is $r=$
{{\left[ {{l}^{2}}-\dfrac{{{\left( {{T}_{0}}/2\pi \right)}^{2}}}{\left\\{ \left( 2\pi /g{{T}_{0}} \right)+\left( qB/mg \right) \right\\}} \right]}^{1/x}}.
Find $x$.
Assume that the string remains in the stretched position.

Answer 1

We can solve this problem by drawing a proper diagram for the situation and analyzing the forces on the ball. Upon analysis, we can get the relation between the different forces and also determine which forces are providing the centripetal force from the equation of which, we can get the radius of the circle as a function of the time period.

Formula used:
${{F}_{C}}=\dfrac{m{{v}^{2}}}{R}$
${{F}_{mag}}=qvB\sin \theta$
$v=R\omega$
$T=\dfrac{2\pi }{\omega }$

Complete step by step answer:
First let us draw a diagram to analyze the problem better.

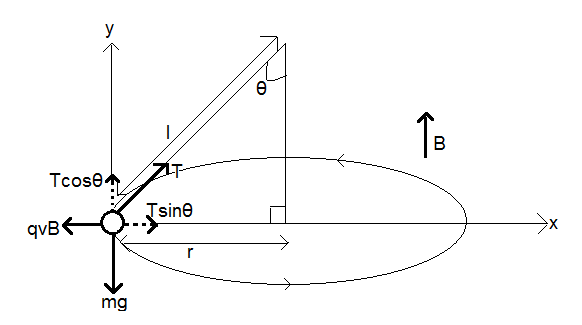
Here as shown, we have two coordinate axes, x and y with the ball rotating around a circle of radius $r$ and currently at the origin position, where the string that it is tied to makes an angle of $\theta$ with the vertical.
The magnetic induction $B$ is in the upward direction.
The charged ball rotates in the sense shown in the figure, that is, anticlockwise.
The length of the string attached is $l$.
The acceleration due to gravity is $g$ and the mass of the ball is $m$.
The tension in the string at this point is $T$ which we have broken into two components along the two axes as shown in the figure, that is, $T\cos \theta$ and $T\sin \theta$.
The ball rotates with a speed $v$ in the circle.
The charge on the ball is $q$.
Let the time period of motion be ${{T}_{0}}$ and the angular frequency be $\omega$.
Due to this motion in the presence of the magnetic field, the charged body experiences a force.
Now, the magnitude of force ${{F}_{mag}}$ experienced by a charged body with charge $q$ having speed $v$ in the presence of a magnetic field of magnitude $B$ is given by
${{F}_{mag}}=qvB\sin \theta$ --(1)
Where $\theta$ is the angle between the velocity and the magnetic field.
The direction of this force is perpendicular to the plane containing the velocity and the magnetic field.
Now, in the figure, we see that the direction of velocity of the ball lies in the horizontal plane while the direction of the magnetic field is upward, that is perpendicular to the velocity. Therefore, the force due to the magnetic field on the charged ball will be always
$qvB\sin {{90}^{0}}=qvB\times 1=qvB$ $\left( \because \sin {{90}^{0}}=1 \right)$ [Using (1)]
The direction of this force will be always towards the outside of the circle on the line joining the centre to the ball due to the sense of rotation (and hence, direction of velocity) of the ball that we have chosen.
This force is represented in the diagram.
Now, for a body of mass $m$ moving in a circular path of radius $R$ with a constant speed $v$, the magnitude of the centripetal force ${{F}_{C}}$ is given by
${{F}_{C}}=\dfrac{m{{v}^{2}}}{R}$ --(2)
For the position of the ball shown in the figure, the centripetal force acts towards the centre of the circle, that is, towards the positive x-direction.

Also, the speed $v$ of a body going about in uniform circular motion in a circular path of radius $R$ is related to its angular frequency $\omega$ by
$v=R\omega$ --(3)
The time period $T$ of uniform circular motion is related to its angular frequency $\omega$ by
$T=\dfrac{2\pi }{\omega }$ --(4)
Now, since the ball only moves in a horizontal circle, it can be said to be in equilibrium along the vertical y axis. Therefore, balancing forces along the y axis and considering forces along the positive y axis to be positive, we get,
$T\cos \theta -mg=0$
$\therefore T\cos \theta =mg$
$\therefore T=\dfrac{mg}{\cos \theta }$ --(5)
Now, along the x-axis we will equate forces with the centripetal force required for the circular motion. We will consider forces towards the positive x-axis to be positive.
Therefore, using (2), we get,
$T\sin \theta -qvB=\dfrac{m{{v}^{2}}}{r}$
Using (5), we get,
$\left( \dfrac{mg}{\cos \theta } \right)\sin \theta -qvB=\dfrac{m{{v}^{2}}}{r}$ -(6)
Now, from the geometry of the figure, we see that
$\sin \theta =\dfrac{r}{l},\cos \theta =\dfrac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l}$
Putting these values in (6), we get
$\left( \dfrac{mg}{\dfrac{\sqrt{{{l}^{2}}-{{r}^{2}}}}{l}} \right)\dfrac{r}{l}-qvB=\dfrac{m{{v}^{2}}}{r}$
$\therefore \dfrac{mgr}{\sqrt{{{l}^{2}}-{{r}^{2}}}}-qvB=\dfrac{m{{v}^{2}}}{R}$
Now, using (3), we get,
$v=r\omega$
Putting this value in the above equation, we get
$\dfrac{mgr}{\sqrt{{{l}^{2}}-{{r}^{2}}}}-qr\omega B=\dfrac{m{{\left( r\omega \right)}^{2}}}{r}=m{{\omega }^{2}}r$
Dividing by $r$ on both sides, we get
$\dfrac{mg}{\sqrt{{{l}^{2}}-{{r}^{2}}}}-q\omega B=m{{\omega }^{2}}$
$\therefore \dfrac{1}{\sqrt{{{l}^{2}}-{{r}^{2}}}}=\dfrac{m{{\omega }^{2}}+q\omega B}{mg}=\dfrac{{{\omega }^{2}}}{g}+\dfrac{q\omega B}{mg}=\dfrac{\omega }{g}\left( \omega +\dfrac{qB}{m} \right)$
Squaring both sides, we get
$\therefore {{\left( \dfrac{1}{\sqrt{{{l}^{2}}-{{r}^{2}}}} \right)}^{2}}={{\left( \dfrac{\omega }{g} \right)}^{2}}{{\left( \omega +\dfrac{qB}{m} \right)}^{2}}$
$\therefore \dfrac{{{1}^{2}}}{{{\left( \sqrt{{{l}^{2}}-{{r}^{2}}} \right)}^{2}}}={{\left( \dfrac{\omega }{g} \right)}^{2}}\left( {{\omega }^{2}}+{{\left( \dfrac{qB}{m} \right)}^{2}}+\dfrac{2qB\omega }{m} \right)=\dfrac{\left( \dfrac{{{\omega }^{2}}}{{{g}^{2}}}+{{\left( \dfrac{qB}{gm} \right)}^{2}}+\dfrac{2qB\omega }{{{g}^{2}}m} \right)}{{{\left( \dfrac{1}{\omega } \right)}^{2}}}$ $\left( \because {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab \right)$
$\therefore \dfrac{1}{{{l}^{2}}-{{r}^{2}}}=\dfrac{\left( {{\left( \dfrac{\omega }{g} \right)}^{2}}+{{\left( \dfrac{qB}{mg} \right)}^{2}}+2\left( \dfrac{\omega }{g} \right)\left( \dfrac{qB}{mg} \right) \right)}{{{\left( \dfrac{1}{\omega } \right)}^{2}}}$
$\therefore \dfrac{1}{{{l}^{2}}-{{r}^{2}}}=\dfrac{{{\left( \dfrac{\omega }{g}+\dfrac{qB}{mg} \right)}^{2}}}{{{\left( \dfrac{1}{\omega } \right)}^{2}}}$
$\left( \because {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab \right)$
$\therefore {{l}^{2}}-{{r}^{2}}=\dfrac{{{\left( \dfrac{1}{\omega } \right)}^{2}}}{{{\left( \dfrac{\omega }{g}+\dfrac{qB}{mg} \right)}^{2}}}$
$\therefore {{r}^{2}}={{l}^{2}}-\dfrac{{{\left( \dfrac{1}{\omega } \right)}^{2}}}{{{\left( \dfrac{\omega }{g}+\dfrac{qB}{mg} \right)}^{2}}}$
Now using (4) in the above equation, we get
$\therefore {{r}^{2}}={{l}^{2}}-\dfrac{{{\left( {{T}_{0}}/2\pi \right)}^{2}}}{{{\left( \dfrac{2\pi }{{{T}_{0}}g}+\dfrac{qB}{mg} \right)}^{2}}}$
Square rooting both sides we get,
$\therefore \sqrt{{{r}^{2}}}=\sqrt{{{l}^{2}}-\dfrac{{{\left( {{T}_{0}}/2\pi \right)}^{2}}}{{{\left( 2\pi /g{{T}_{0}}+qB/mg \right)}^{2}}}}$
\therefore r={{\left( {{l}^{2}}-\dfrac{{{\left( {{T}_{0}}/2\pi \right)}^{2}}}{\left\\{ \left( 2\pi /g{{T}_{0}} \right)+\left( qB/mg \right) \right\\}} \right)}^{\dfrac{1}{2}}}
Comparing with the value given in the question
{{\left[ {{l}^{2}}-\dfrac{{{\left( {{T}_{0}}/2\pi \right)}^{2}}}{\left\\{ \left( 2\pi /g{{T}_{0}} \right)+\left( qB/mg \right) \right\\}} \right]}^{1/x}}={{\left[ {{l}^{2}}-\dfrac{{{\left( {{T}_{0}}/2\pi \right)}^{2}}}{\left\\{ \left( 2\pi /g{{T}_{0}} \right)+\left( qB/mg \right) \right\\}} \right]}^{1/2}}
$\therefore \dfrac{1}{x}=\dfrac{1}{2}$
$x=2$
Therefore, the required value of $x$ is $2$.

Note: This problem seems like a complex one. However, actually it is a simple problem which involves only analyzing the proper force equations and equating the forces. What makes the problem complex is its difficult calculation and the various manipulation of the variables and the equations that are required to get to the correct answer. However, students must notice the form of the equation given in the question and base their manipulation upon getting closer to that form with each step. This will make the calculation a bit simpler and provide a direction in which the student must proceed with the calculation.