Question

A small bulb is placed at the bottom of a tank containing water to a depth of $80\,cm$ . What is the area of the surface of water through which light from the bulb can emerge? Refractive index of water is $1.33$ (Consider the bulb to a point source)
A. $2.6\,{m^2}$
B. $3.6\,{m^2}$
C. $4.2\,{m^2}$
D. $5.8\,{m^2}$

Answer 1

In order to solve this question we have to understand the critical angle of refraction. Critical angle of refraction is that angle of incidence which upon incident of medium get refracted along the interface and for angle greater than critical angle light incident would be totally reflected in the same medium. Also light always travels by forming a cone which on the projection of the plane is a triangle.

Complete step by step answer:
Due to point source at the bottom of the lake light travels inside water and when it falls at the interface of water it gets refracted and reflected at medium but for viewing a complete light beam it must fall on a critical angle so that after refraction it travels along the interface thereby not blocking any vision. Let the light incident at angle $i$.

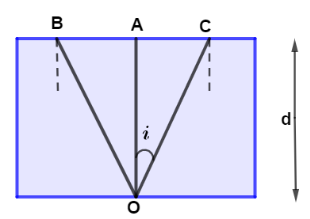
Given in question refractive index is $\mu = 1.33$ and depth $OA = 80cm$
So by using Snell law we get
$\mu = \dfrac{{\sin 90^\circ }}{{\sin i}} = \dfrac{1}{{\sin i}}$
$\Rightarrow \sin i = \dfrac{1}{\mu }$ So putting values in expression we get
$\Rightarrow \sin i = \dfrac{1}{{1.33}} = 0.752$
$\Rightarrow i = {\sin ^{ - 1}}(0.752) = 48.76^\circ$
Now using trigonometry in $\Delta OAC$ We get $\tan i = \dfrac{{AC}}{{OA}}$
$AC = OA \times \tan i$
Putting values we get
$AC = 80\,cm \times \tan (48.76)$
$\Rightarrow AC = 91.254\,cm = 0.912\,m$
Hence the radius of beam is $R = AC = 0.912\,m$
Hence area of beam is $A = \pi {R^2}$
Putting values we get
$A = \pi \times {(0.912)^2}$
$\therefore A= 2.613\,{m^2}$

Therefore, the correct answer is (A).

Note: It should be remembered that we have chosen a critical angle so as to view the complete beam emerging out from the surface of water as a perfect light cone. Also the radius is equal to AC because when the cone is projected in $2 - D$ space on the surface of water then it forms a triangle having base length equal to diameter.