Question

A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)

Answer 1

To solve this question of total internal refraction, we can approach this question geometrically. Let us form an illustration of the given conditions

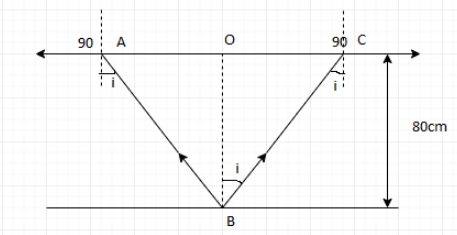
From the figure, when we assume that the bulb is placed at point B ,it is evident that in order to find the area of surface through which the light emerges, we have to find the area of the circle with radius OA.

Formulas used:
Refractive index $\mu =\dfrac{\sin i}{\sin r}$, where I is the angle of incidence and r is the angle of refraction of the ray that we consider.

Complete step by step answer:
We’re given that, the depth of the tank is d1=$80cm=0.8m$
We also know that the refractive index of water $\mu =1.33$
Let us consider the radius to be $R=\dfrac{AC}{2}$
We know that Refractive index $\mu =\dfrac{\sin i}{\sin r}$,
Here,$\mu =\dfrac{\sin 90}{\sin i}$
$\Rightarrow i={{48.75}^{\circ }}$
When we consider $\vartriangle OBC$from the figure,
$\tan i=\dfrac{OC}{OB}=\dfrac{R}{d1} \\\ \Rightarrow R=0.91 \\\$
Now that we’ve obtained the radius, we can find the area of the circle using the formula,
$\therefore A=\pi {{R}^{2}}=\pi {{(0.91)}^{2}}=2.61{{m}^{2}}$
Hence the the area of surface through which the light emerges is $2.61{{m}^{2}}$.

Note: Refractive index is an essential parameter as far as liquids are concerned. We can analyse parameters like dispersion, purity, and diffusion coefficient of liquids with the help of a refractive index. Refractive index is applied in daily life as it is used in instruments like glasses, cameras, microscopes etc.