Question

A small boy is throwing a ball towards a wall 6m in front of him. He releases the ball at a height of $1.4m$ from the ground. The ball bounces from the wall at a height of $3m$ , rebounds from the ground and reaches the boy's hand exactly at the point of release. Assuming the two bounces (one from the wall and the other from the ground) to be perfectly elastic, how far ahead of the boy did the ball bounce from the ground?
A) $1.5\,m$
B) $2.5\,m$
C) $3.5\,m$
D) $4.5\,m$

Answer 1

In this solution, we will use the relation of kinematics to determine the distance between the ball bounce and the boy. We will break the components of velocity of the ball into parallel and perpendicular components with respect to the ground.

Formula used: In this solution, we will use the following formula:
- First equation of kinematics: $v = u + at$ where $v$ is the final velocity of the object
- Second equation of kinematics: $d = ut + \dfrac{1}{2}a{t^2}$ where $d$ is the distance travelled by the object with initial velocity $u$ under acceleration $a$ in time $t$

Complete step by step answer

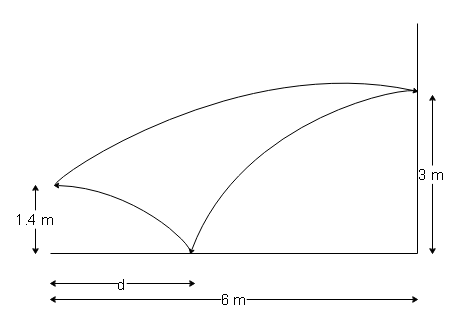
Let the horizontal velocity of the boy be $u$ and the vertical velocity will be $v$ .
When the boy throws the ball, the ball travels a distance of 6 metres. The time it will take to cover this horizontal distance will be dependent on the horizontal velocity and can be calculated as:
${t_1} = \dfrac{6}{u}$
At this time, the ball covers a horizontal distance $\Delta y = 3 - 1.4 = 1.6\,m$ . The initial perpendicular velocity $v$ of the ball in the vertical direction can be calculated using the second law of kinematics as:
$1.6 = v{t_1} + \dfrac{1}{2}gt_1^2$
Or,
$1.6 = v\dfrac{6}{u} + \dfrac{1}{2}g{\left( {\dfrac{6}{u}} \right)^2}$
Now when the ball strikes the ball, the collision is elastic so the vertical component of the ball’s velocity will be the same but the horizontal velocity will change its direction.
While the ball is falling back towards the ground and going towards the boy after bouncing, the time taken by the ball to reach a height from $1.4\,m$ (starting from $1.6\,m$ ) will be the same as its initial vertical velocity $v$ but with a negative direction since it falling towards the ground.
The time taken to reach $1.4\,m$ will be
${t_2} = \dfrac{{12 - 2d}}{u}$
Using the time of flight formula, we can write
$\dfrac{v}{5} = \dfrac{{12 - 2d}}{u}$
We can see from the diagram that the time the ball will take to reach the boy from this point will be ${t_2} = \dfrac{d}{u}$ where $d$ is the distance of the ball when it makes the first bounce with the boy. The vertical speed will be $- v$ .
So using the second law of kinematics from the point where the ball is at a height of $1.4\,m$ , we get
$- 1.4 = - v\dfrac{d}{u} - 5{\left( {\dfrac{d}{u}} \right)^2}$
Substituting equation (1) and (2) in the above equation, we get
$1.6 = \dfrac{{6(60 - 10d) - 180}}{{{u^2}}}$
And
$8.4{u^2} = (4.6{u^2} + 180)d + 30{d^2}$
Substituting equation (3) in equation (4), we get
$30{d^2} - 675d + 945 = 0$
Which gives us
$d = 21\,m\,{\text{or}}\,{\text{d = 1}}{\text{.5}}\,{\text{m}}$
Since $d = 21\,m$ isn’t possible as in this case, the ball will bounce behind the person, $d = 1.5\,m$ which is the correct choice that corresponds to option (A).

Note
We should realize to split the velocities into horizontal and vertical components which will simplify our calculations very much. While using the equation of kinematics, we should realize to use proper sign convention i.e. up as positive and down as negative.