Question

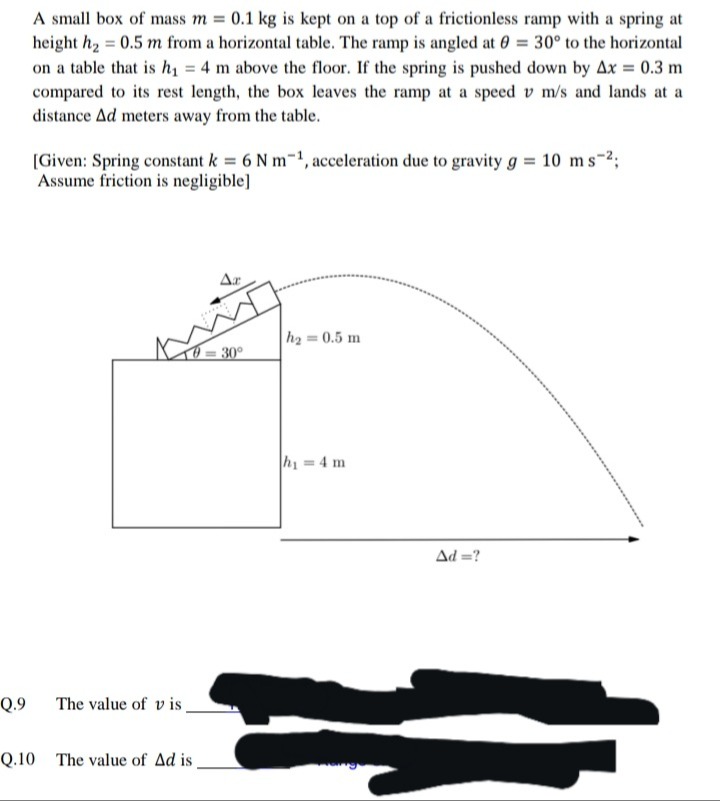
A small box of mass $m = 0.1$ kg is kept on a top of a frictionless ramp with a spring at height $h_2 = 0.5$ m from a horizontal table. The ramp is angled at $\theta = 30^\circ$ to the horizontal on a table that is $h_1 = 4$ m above the floor. If the spring is pushed down by $\Delta x = 0.3$ m compared to its rest length, the box leaves the ramp at a speed $v$ m/s and lands at a distance $\Delta d$ meters away from the table.

[Given: Spring constant $k = 6$ N m$^{-1}$, acceleration due to gravity $g = 10$ m s$^{-2}$; Assume friction is negligible]

Answer 1

Q.9: 1.55 Q.10: 1.38

Answer 2

Q.9: We use the principle of conservation of energy to find the speed $v$ of the box when it leaves the ramp.

Initial energy:
Spring potential energy $U_{si} = \frac{1}{2}k(\Delta x)^2$

Final energy:
Kinetic energy $K_f = \frac{1}{2}mv^2$
Gravitational potential energy $U_{gf} = mg(\Delta x \sin\theta)$

By conservation of energy: $\frac{1}{2}k(\Delta x)^2 = \frac{1}{2}mv^2 + mg(\Delta x \sin\theta)$
$v^2 = \frac{k(\Delta x)^2}{m} - 2g \Delta x \sin\theta$

Given values: $m = 0.1$ kg, $k = 6$ N m$^{-1}$, $\Delta x = 0.3$ m, $g = 10$ m s$^{-2}$, $\theta = 30^\circ$.
$\sin\theta = \sin 30^\circ = \frac{1}{2}$.
$v^2 = \frac{6 \times (0.3)^2}{0.1} - 2 \times 10 \times 0.3 \times \frac{1}{2} = 5.4 - 3 = 2.4$
$v = \sqrt{2.4} \approx 1.55$ m/s

Q.10: The box leaves the ramp at a speed $v = \sqrt{2.4}$ m/s at an angle $\theta = 30^\circ$ above the horizontal. The initial height of the box above the floor is $H = h_1 + h_2 = 4 + 0.5 = 4.5$ m.

Initial velocity components:
$v_x = v \cos\theta = \sqrt{2.4} \cos 30^\circ = \sqrt{2.4} \times \frac{\sqrt{3}}{2} = \sqrt{1.8}$ m/s
$v_y = v \sin\theta = \sqrt{2.4} \sin 30^\circ = \sqrt{2.4} \times \frac{1}{2} = \sqrt{0.6}$ m/s

The horizontal distance is $\Delta d = v_x \times t$, where $t$ is the time of flight.
The vertical motion is described by $y_f = y_0 + v_{y0}t + \frac{1}{2}a_yt^2$.
Here, $y_0 = H = 4.5$ m, $y_f = 0$, $v_{y0} = v_y = \sqrt{0.6}$ m/s, $a_y = -g = -10$ m/s$^2$.
$0 = 4.5 + \sqrt{0.6}t - 5t^2$
$5t^2 - \sqrt{0.6}t - 4.5 = 0$

Using the quadratic formula $t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:
$a = 5$, $b = -\sqrt{0.6}$, $c = -4.5$
$t = \frac{\sqrt{0.6} \pm \sqrt{(-\sqrt{0.6})^2 - 4(5)(-4.5)}}{2(5)} = \frac{\sqrt{0.6} + \sqrt{90.6}}{10} \approx 1.0293$

Now, calculate $\Delta d = v_x \times t = \sqrt{1.8} \times \frac{\sqrt{0.6} + \sqrt{90.6}}{10} \approx 1.3810 \approx 1.38$ m