Question

A small body of super dense material, whose mass is twice the mass of Earth but whose size is very small compared to the size of Earth starts from rest at a height $H < < R$ above the Earth’s surface and reaches the surface in time t. Then t is equal to
A. $\sqrt {\dfrac{{2H}}{g}}$
B. $\sqrt {\dfrac{H}{g}}$
C. $\sqrt {\dfrac{{2H}}{{3g}}}$
D. $\sqrt {\dfrac{{4H}}{{3g}}}$

Answer 1

Here we shall use the concept of center of mass. In any system if the bodies are in motion, the motion is executed so as to keep the center of mass constant. In this question, first we will find out the distance the heavier mass has to travel to keep the center of mass constant. Then we shall apply the formula of the time taken when an object is under free fall. Making proper substitutions, we will get the answer.

Formula used: We shall use the formula $t = \sqrt {\dfrac{{2s}}{g}}$ where t is the time taken, s is the distance covered and g is the acceleration due to gravity.

Complete step by step solution:
Let’s visualize the situation first.

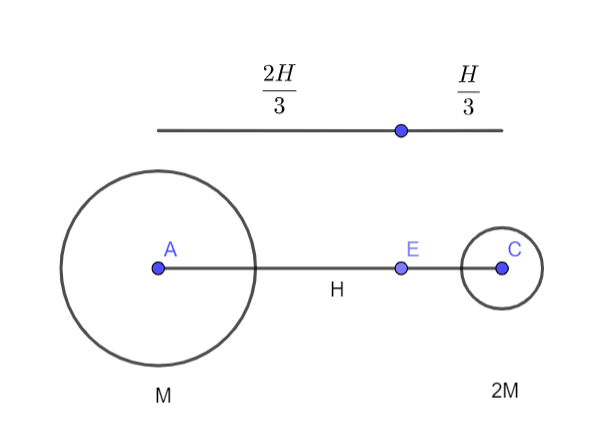
For locating the center of mass, we shall assume the whole length be H units. Since the masses are in the ratio $2:1$ , the center of mass will lie closer to the body having bigger mass. So, the distance between the center of mass and the heavier body will be lesser.
Let’s assume the center of mass to lie at point E. Now, the distance between the center of mass and the heavier body will be given by $l = \dfrac{{1 \times H}}{{2 + 1}} = \dfrac{H}{3}$
The distance between the center of mass and the lighter body will be given by $H - l = H - \dfrac{H}{3}$
$H - l = \dfrac{{2H}}{3}$
For the center of mass to remain constant, the heavier body will have to move a distance of $\dfrac{H}{3}$ .
Since no initial velocity is given for the heavier mass, we shall assume it to be zero. Thus, it becomes a free fall situation.
We know that the time taken by a body when the object is under free fall is given by $t = \sqrt {\dfrac{{2s}}{g}}$ where t is the time taken, s is the distance covered and g is the acceleration due to gravity.
Here, $s = \dfrac{H}{3}$ .
Substituting in the formula we get,
$t = \sqrt {\dfrac{{2 \times \dfrac{H}{3}}}{g}}$
Further solving this we get,
$t = \sqrt {\dfrac{{2H}}{{3g}}}$
Hence, option C is the correct answer.

Note:
Here we directly used the formula $t = \sqrt {\dfrac{{2s}}{g}}$ since there were no constraints on the initial velocity and it became a standard case of free fall. However, in cases when some initial velocity is specified for the objects, we have to use one of the speed equations to get the time taken. We keep the center of mass constant for the equilibrium to exist. In this case, it will be the neutral equilibrium.