Question
Question: A small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The ot...
A small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O (figure shown above) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r=r0 the angular velocity of the thread is equal to ωo.
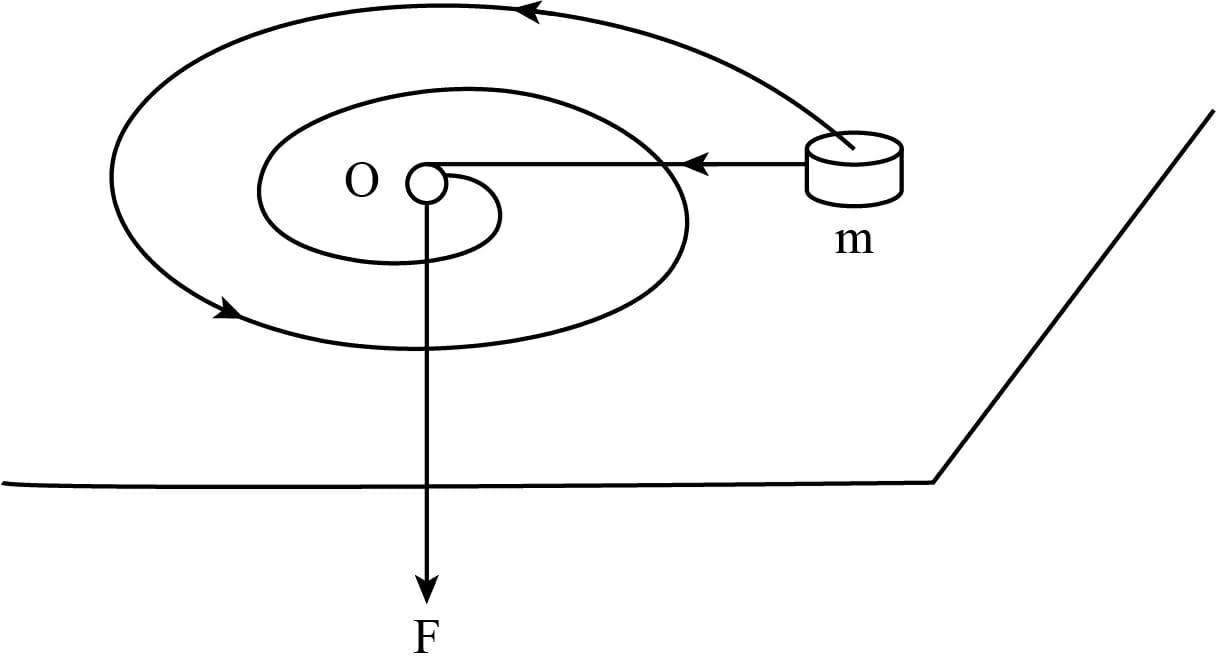
Solution
To solve this problem we use the concept of conservation of angular momentum since the momentum of force T is also zero at the point O. Therefore, we can say that the angular momentum of the particle m is conserved about the centre point O.
Complete step by step answer:
Forces, acting on the mass m are shown in the figure. As a vector N = mg, the net torque of these two forces about any fixed point must be equal to zero. Tension T, acting on the mass m is a central force, which is always directed towards the centre O. Hence the moment of force T is also zero about the point O and therefore the angular momentum of the particle m is conserved about O.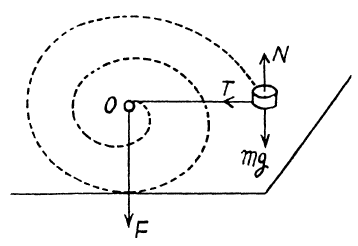
Let, the angular velocity of the particle be ω, when the separation between hole and particle m is r, then from the conservation of angular momentum about the point O,
∴m(ωoro)ro=m(ωr)r
Also ω=r2ωoro2
Now from the Newton’s second law of motion,
T = F = mω2r
⇒F = r4mωo2ro4r=r3mωo2ro4
∴ The thread tension = r3mωo2ro4
Note:
Law of conservation of angular momentum states that if no external torque acts on the object, then there is no angular momentum.
∵torque (τ) = dTdL
L = angular momentum
Because the momentum of τ is zero.
⇒τ=0
⇒dtdL=0
⇒L = 0
So, the angular momentum is conserved.
∴m(ωr)r = m(ωoro)ro
