Question

A small body of mass m slides without friction from the top of a hemisphere of radius $R$ . At what height will the body be detached from the center of the hemisphere?

A. $h = \dfrac{r}{2}$
B. $h = \dfrac{r}{3}$
C. $h = \dfrac{{2r}}{3}$
D. $h = \dfrac{r}{4}$

Answer 1

Frictional force always behaves parallel to two planes that are in contact with each other and in a direction opposite to that of relative motion of the two bodies. It always decreases the relative motion between two bodies or surfaces. The frictional force is higher for rough surfaces and less for smooth surfaces.

Complete step by step solution:

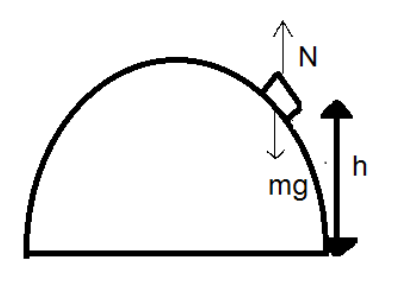
From the diagram
$mg\cos \theta - N = \dfrac{{m{v^2}}}{2}$ ………………. (1)
When the body is detached $N = 0$ then
Equation (1) becomes,$mg\cos \theta = \dfrac{{m{v^2}}}{2}$
$g\cos \theta = \dfrac{{{v^2}}}{2}$
$\cos \theta = \dfrac{{{v^2}}}{{2g}}$ …………….. (2)
By applying the conservation law of mechanical energy
$Ki + Vi = Kf + Vf$ …………. (3)
Where initial $Ki = 0$ and $Vi = mgr(1 - \cos \theta )$
Final $Kf = \dfrac{1}{2}m{v^2}$ and $Vf = 0$
By putting these values in equation (3)
We get $0 + mgr(1 - \cos \theta ) = \dfrac{1}{2}m{v^2} + 0$
$\Rightarrow gr(1 - \cos \theta ) = \dfrac{1}{2}{v^2}$
$\Rightarrow (1 - \cos \theta ) = \dfrac{{{v^2}}}{{2gr}}$ …………….. (2)
From equation (2) and (3)
We get
$2(1 - \cos \theta ) = \cos \theta$
$\cos \theta = \dfrac{2}{3}$
So height, $h = r\cos \theta$
$\Rightarrow h = \dfrac{{2r}}{3}$
So the correct option is C .

Note:
There are four types of friction, 1) static friction: when one body slides over a surface of another body is known as static friction. 2)Dynamic Friction: The frictional force which is efficient when two surfaces in contact with each other are in relative motion concerning each other is known as dynamic friction. 3) Sliding friction: This frictional force is present when one body slides over another. 4) Rolling Friction: It can be defined as the opposite force on a rolling body.