Question

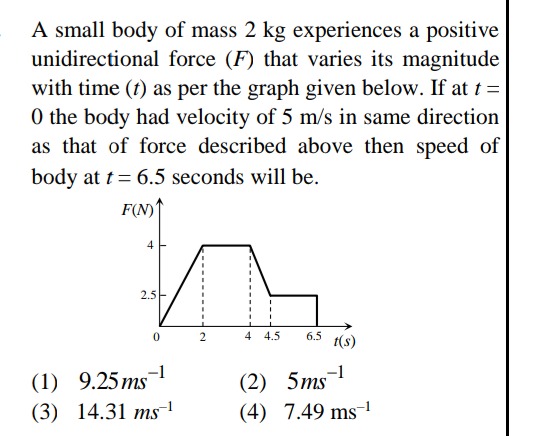
A small body of mass 2 kg experiences a positive unidirectional force (F) that varies its magnitude with time (t) as per the graph given below. If at t = 0 the body had velocity of 5 m/s in same direction as that of force described above then speed of body at t = 6.5 seconds will be.

• A. 9.25 $ms^{-1}$
• B. 5$ms^{-1}$
• C. 14.31 $ms^{-1}$
• D. 7.49 $ms^{-1}$

Answer 1

Answer: (C)

14.3125 m/s

Answer 2

The change in momentum of the body is equal to the impulse delivered by the force. The impulse is the area under the Force-time (F-t) graph.

The F-t graph can be divided into four regions:

1. Region 1 (0 to 2 s): A triangle with base 2 s and height 4 N. Area$_1 = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 2 \, \text{s} \times 4 \, \text{N} = 4 \, \text{Ns}$.
2. Region 2 (2 to 4 s): A rectangle with base (4 - 2) = 2 s and height 4 N. Area$_2 = \text{base} \times \text{height} = 2 \, \text{s} \times 4 \, \text{N} = 8 \, \text{Ns}$.
3. Region 3 (4 to 4.5 s): A trapezoid with parallel sides 4 N and 2.5 N, and height (4.5 - 4) = 0.5 s. Area$_3 = \frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height} = \frac{1}{2} \times (4 \, \text{N} + 2.5 \, \text{N}) \times 0.5 \, \text{s} = \frac{1}{2} \times 6.5 \, \text{N} \times 0.5 \, \text{s} = 1.625 \, \text{Ns}$.
4. Region 4 (4.5 to 6.5 s): A rectangle with base (6.5 - 4.5) = 2 s and height 2.5 N. Area$_4 = \text{base} \times \text{height} = 2 \, \text{s} \times 2.5 \, \text{N} = 5 \, \text{Ns}$.

The total impulse ($J$) is the sum of these areas: $J = \text{Area}_1 + \text{Area}_2 + \text{Area}_3 + \text{Area}_4 = 4 \, \text{Ns} + 8 \, \text{Ns} + 1.625 \, \text{Ns} + 5 \, \text{Ns} = 18.625 \, \text{Ns}$.

According to the impulse-momentum theorem: $J = \Delta p = m(v_f - v_i)$ Given mass $m = 2$ kg and initial velocity $v_i = 5$ m/s. $18.625 \, \text{Ns} = 2 \, \text{kg} \times (v_f - 5 \, \text{m/s})$ $v_f - 5 \, \text{m/s} = \frac{18.625 \, \text{Ns}}{2 \, \text{kg}} = 9.3125 \, \text{m/s}$ $v_f = 5 \, \text{m/s} + 9.3125 \, \text{m/s} = 14.3125 \, \text{m/s}$.

Since the force is always positive and the initial velocity is in the same direction, the velocity remains positive, so the speed is equal to the velocity. The speed of the body at t = 6.5 seconds will be 14.3125 m/s.