Question

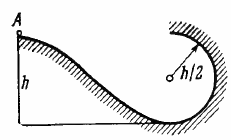
A small body A starts sliding from the height ′h′ down an inclined groove passing into a half-circle of radius 2h​(figure shown above). Assuming the friction to be negligible, find the velocity of the body at the highest point of its trajectory (after breaking off the groove).

Answer 1

In this question we are going to learn about the conservation of energy and about motion, its second equation including the concepts and the equations as well as formulas behind it. And by using this information, we can easily approach our answer. Below here we have explained each and every topic thoroughly, let us take them one by one.

Complete step by step answer:
The conservation of mechanical energy: whenever in a solar system a mechanical process comes into consideration potential and kinetic energies are always mentioned.
Conservation of mechanical energy tells us that the total mechanical energy present in a system (i.e., the sum of the potential plus kinetic energies) remains the same until the only forces acting are conservative forces.
Motion: Motion is any difference in an object position due a course of time. We all have gone through terms like velocity, acceleration, speed. These all quantities always tell us about motion. Whenever we describe motion, we always use a frame of reference like we use context relative to which we say that motion has been occurring. A motionless object or stationary object is that object which shows no change with the frame of reference.
The second equation of motion is mathematically:
$s = ut + \dfrac{1}{2}a{t^2}$
This equation of motion allows us to make a relation between time, distance, initial velocity and acceleration.

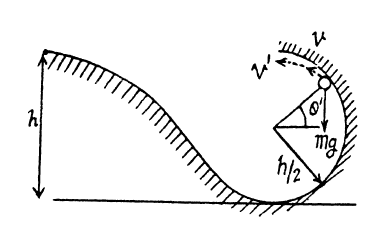
The radius of vertical track is R, so to finish a smooth vertical track the minimum height at which a particle begins, must be the same quantity to $\dfrac{5}{2}R$. So, we can conclude that in our problem the body will not be touching the highest point of the vertical track of radius $\dfrac{R}{2}$. Imagine particle A taking off the track at some point O with speed v (figure shown below). Now putting in account energy conservation for the body A in the field of gravity
$mg[h - \dfrac{h}{2}(1 + \sin \theta )] = \dfrac{1}{2}m{v^2}$
${v^2} = gh(1 - \sin \theta )$……………. (1)
By using Newton’s second law at point O for the particle, ${F_n} = m{w_n}$
$N + mg\sin \theta = \dfrac{{m{v^2}}}{{(\dfrac{h}{2})}}$
As we can say that at point O the normal reaction N = 0
${v^2} = \dfrac{{gh}}{2}\sin \theta$…………. (2)
By understanding equation 1 and 2, $\sin \theta = \dfrac{2}{3}$ and $v = \sqrt {\dfrac{{gh}}{3}}$
Now after departing from the track at O, the particle A will appear in the air and then go up. When it has attained the maximum height of its path in air, it's velocity (say v′) appears as horizontal (figure shown below). So, we can conclude that velocity at point A
$v' = v\cos (90 - \theta ) = v\sin \theta = \dfrac{2}{3}\sqrt {\dfrac{{gh}}{3}}$

Note:
In this we learned about motion, its second equation of motion. We also learned about the concept of conservation of energy. Now we can use that knowledge in further questions. We have learned in this question many concepts of physics, which will always be helpful.